Найти острые углы прямоугольного треугольника, площадь которого равна 8 и гипотенуза равна 8.

1 ответ

Посмотреть ответы

DevAdmin

1690

Ответ:

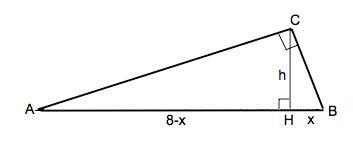
Объяснение: Назовем треугольник АВС; угол С=90°, АВ=8, Ѕ(АВС)=8, СН- высота.
—————
Одна из формул площади треугольника Ѕ=h•a/2, где h- высота, а - сторона, к которой высота проведена. Тогда 8=h•8/2, => h=2
Высота, которую провели из прямого угла на гипотенузу треугольника, равна среднему геометрическому проекций обоих катетов на эту гипотенузу ( т.е. отрезков, на которые она её делит).
Примем ВН=х. Тогда АН=8-х (см. рисунок).
СН²=ВН•АН
4=х•(8-х)⇒
х²-8х+4=0.
Решив квадратное уравнение, получим х₁=7,4641; х₂=0,5359
AH- больший отрезок, равен х₁=7,4641
tgA=CH:AH=2:7,4641=0,267949
∠ А=arctg 0,267949 ( по таблице Брадиса или калькулятору это угол 15°).
Из суммы острых углов прямоугольного тр-ка ∠ В=90°-15°=75°

Хороший ответ

4 апреля 2023 17:07

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Точки D (1; 4) и E (2; 2) — середины сторон AC и BC треугольника ABC соответственно. Чему равны координаты вершины C, если В (-3; -1)? *один правильн... Известно, что площадь ромба равна половине произведения его диагоналей. Найдите диагонали ромба, если одна из них в 1,5 раза меньше другой, а площадь... Углы DEF и MEF - смежные, луч EK - биссектриса угла DEF, угол KEF на 78° меньше угла MEF. Найдите углы DEF и MEF.... Увеличилось основание цилиндра радиусом 6 см и высоту цилиндра на 5 см. Если начальный объем равен 720 см, во сколько раз увеличится площадь боковой п... Построить треугольник по стороне и двум прилежащим к ней углам...