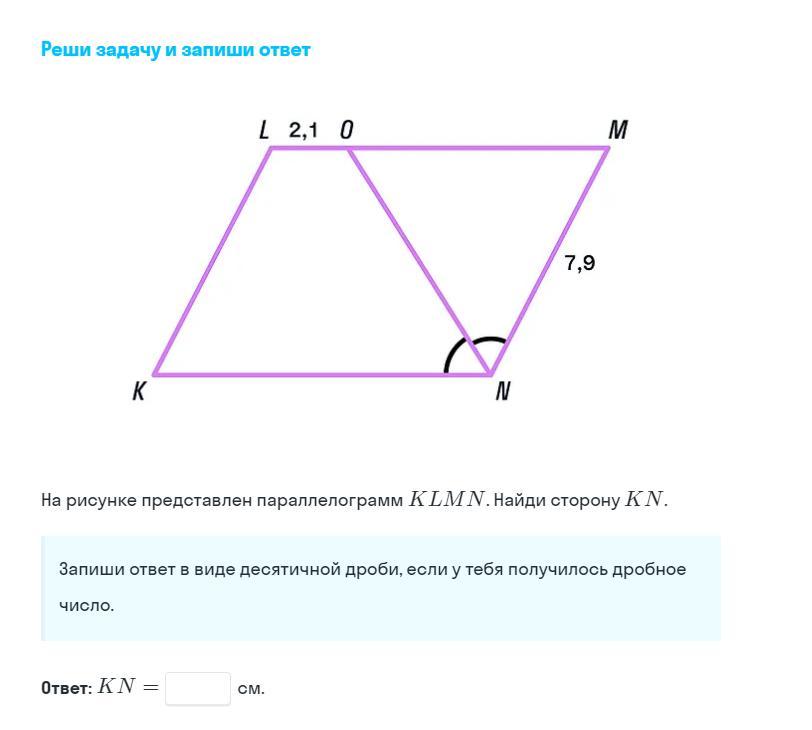
На рисунке представлен параллелограмм KLMN. Найдите сторону KN

1 ответ

Посмотреть ответы

DevAdmin

1700

Ответ:
Сторона KN равна 10 единиц
Объяснение:
Дано: KLMN - параллелограмм, MN = 7,9; LO = 2,1; ∠KNO = ∠MNO
Найти: KN - ?
Решение:
Так как по условию KLMN - параллелограмм, то по определению параллелограмма его противоположные стороны параллельны, следовательно LM║KN.
Угол ∠KNO = ∠MON как накрест лежащие углы при секущей по теореме, так как LM║KN, а ON - секущая.
Так как ∠KNO = ∠MON и по условию ∠KNO = ∠MNO, то
∠MNO = ∠MON, следовательно треугольник ΔOMN - равнобедренный.
Так как треугольник ΔOMN - равнобедренный, то по определению равнобедренного треугольника OM = MN = 7,9.
По основному свойству отрезка:
LM = LO + OM = 2,1 + 7,9 = 10.
Так как по условию KLMN - параллелограмм, то по свойствам параллелограмма его противоположные стороны равны, тогда
KN = LM = 10.
#SPJ3

Хороший ответ

4 апреля 2023 18:36

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Отрезки MN и EF пересекаются в их середине P . Докажите, что EN//MF... Основание пирамиды - ромб с тупым углом α. Все двугранные углы при основании пирамиды равны β. Найдите площать полной поверхности пирамиды, если её вы... Вычислите угол между прямыми AB и CD, если A (√3;1;0), B(0;0;2√2), С(0;2;0), D(√3,1;2√2).... Сфера задана уравнением Х^2+У^2+Z^2-2y-4z=4 А) найти координаты центра и радиус сферы... Одна из сторон параллелограмма в 4 раза больше другой.Найдите длину меньшей стороны,если периметр параллелограмма равен 30 см....