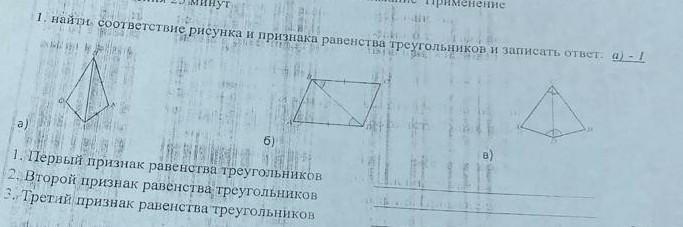
1. найти соответствие рисунка и признака равенства треугольников и записать ответ. a) Б. І а) б) в) 1. Первый признак равенства треугольников 2. Второй признак равенства треугольников 3. Третий признак равенства треугольниковПОЖАЛУЙСТА ОЧЕНЬ СРОЧНО!!!

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
а) - 3
б) - 1
в) - 2
Объяснение:
Первый признак равенства треугольников:

если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства треугольников:

если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников:

если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

а) AB = CB, AD = CD, BD - общая сторона, значит
ΔABD = ΔCBD по трем сторонам (по третьему признаку)

б) AD = BC, ∠ADB = ∠CBD, BD - общая сторона, значит
ΔADB = ΔCBD по двум сторонам и углу между ними (по первому признаку)

в) ∠ACD = ∠BCD, ∠ADC = ∠BDC, CD - общая сторона, значит
ΔACD = ΔBCD по стороне и двум прилежащим к ней углам (по второму признаку)

Хороший ответ

4 апреля 2023 19:58

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В прямоугольном треугольнике PKT(угол Т=90 градусов), РТ=7 корней из 3,КТ=7 см. Найдите угол К и гипотенузу КР... В треугольнике ABC стороны AC и BC равны. Внешний угол при вершине C равен 78°.найдите угол B. Ответ дайте в градусах... Сформулируйте основные свойства расположения точек относительно прямой на плоскости... 1)на стороне ad параллелограмма взята точка e так,что AE =4 см ЕД =5см ВЕ=12см ВД=13см найти S параллелограмма 2)В остроугольном треугольнеке ABC пров... 1.Запишите формулы площади треугольника 2-мя способами рис 29( фото вложила) 2.Найдите площадь треугольника MPK, используя рисунок 31(фото вложила). П...