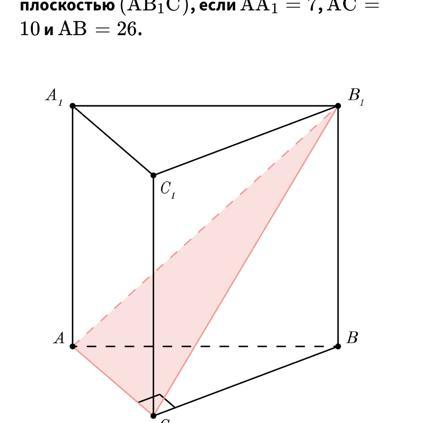
Найди площадь сечения прямой призмы плоскостью (AB1C), если AA1=7, AC=10 и AB=26

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:
125 ед²

Решение:
∆АВС- прямоугольный треугольник
По теореме Пифагора
ВС=√(АВ²-АС²)=√(26²-10²)=
=√(676-100)=√576=24 ед.
ВВ1=АА1=7ед
∆В1ВС- прямоугольный треугольник
По теореме Пифагора
В1С=√(В1В²+ВС²)=√(7²+24²)=
=√(49+576)=√625=25 ед.
ВС перпендикулярно АС, → В1С перпендикулярно АС, Теорема о трех перпендикулярах.
∆АСВ1- прямоугольный треугольник
S(∆ACB1)=½*AC*CB1=10*25/2=
=125 ед²

Хороший ответ

4 апреля 2023 20:06

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В прямоугольной трапеции ABCD(угол A=90°) известно, что AB=4см, AD=15 см, BC=12см. Найдите величину |вектор AB- вектор AD+ вектор BC|.... Заданы стороны треугольников. Выберите все прямоугольные треугольники... Практические способы построения параллельных прямых. Срочно нужно! Помогите!... Диагонали ромба равны 14 см и 48 см . Найдите сторону ромба и его площадь... Прямая MC перпендикулярна плоскости прямоугольника ABCD. Найдите расстояние от точки M до точки пересечения диагоналей прямоугольника ABCD, если AB =...