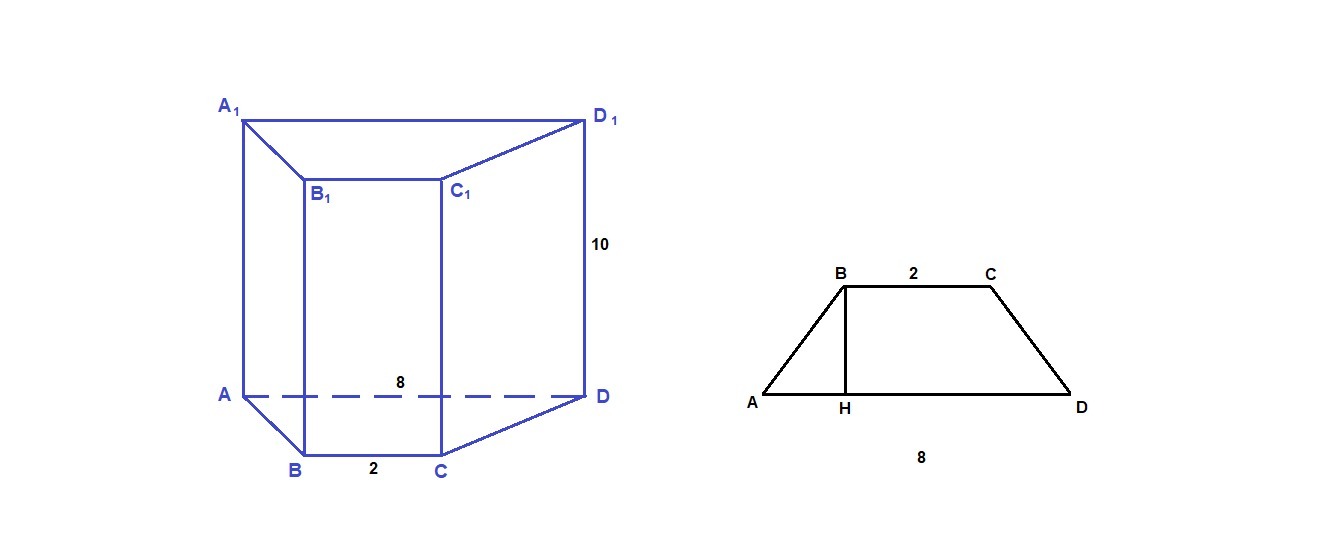
1 . Боковое ребро прямой призмы равно 10 см , а ее объем - 200 см3 . Основание призмы - равнобокая трапеция с основаниями 2 и 8 см . Найдите полную поверхность призмы

1 ответ

Посмотреть ответы

DevAdmin

1690

Объем призмы:
V = Sосн · AA₁
200 = Sосн · 10
Sосн = 200/10 = 20 см²
Sосн = (AD + BC)/2 · BH
20 = (8 + 2)/2 · BH
20 = 5 · BH
BH = 4 см
Высота в равнобедренной трапеции делит большее основание на отрезки, один из которых равен полусумме оснований (больший), а другой - полуразности оснований.
АН = (AD - BC)/2 = (8 - 2)/2 = 3 см
ΔАВН - прямоугольный, египетский, значит АВ = 5 см
Sполн = Sбок + 2Sосн
Sбок = Росн · АА₁ = (8 + 2 + 5 · 2) · 10 = 200 см²
Sполн = 200 + 2 · 20 = 240 см²

Хороший ответ

4 апреля 2023 23:35

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

A1Чему равна сумма внутренних углов выпуклого n-угольника 1)180°⋅(n-2) 2)180°⋅(n+2) 3)180°⋅n 4)180°;n обосновать ответ A2Чему равна сумма углов... 1. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол между диагоналями, если угол ABO равен 50 градусов.... Один из углов равнобедренного треугольника равен 96* .найдите два других угла... Боковая сторона трапеции равна 5 , а один из прилегающих к ней углов равен 30 гр-сов .Найдите площадь трапеции,если ее основания равны 3 и 9?)... Осевая симметрия Нарисуйте четырехугольник, и рядом проводите линию. К ней от каждой точки проводите перпендикуляр, и продолжайте на ту же длину. По...