Вычислите:cos(17π/6) (подробное объяснение пожалуйста)

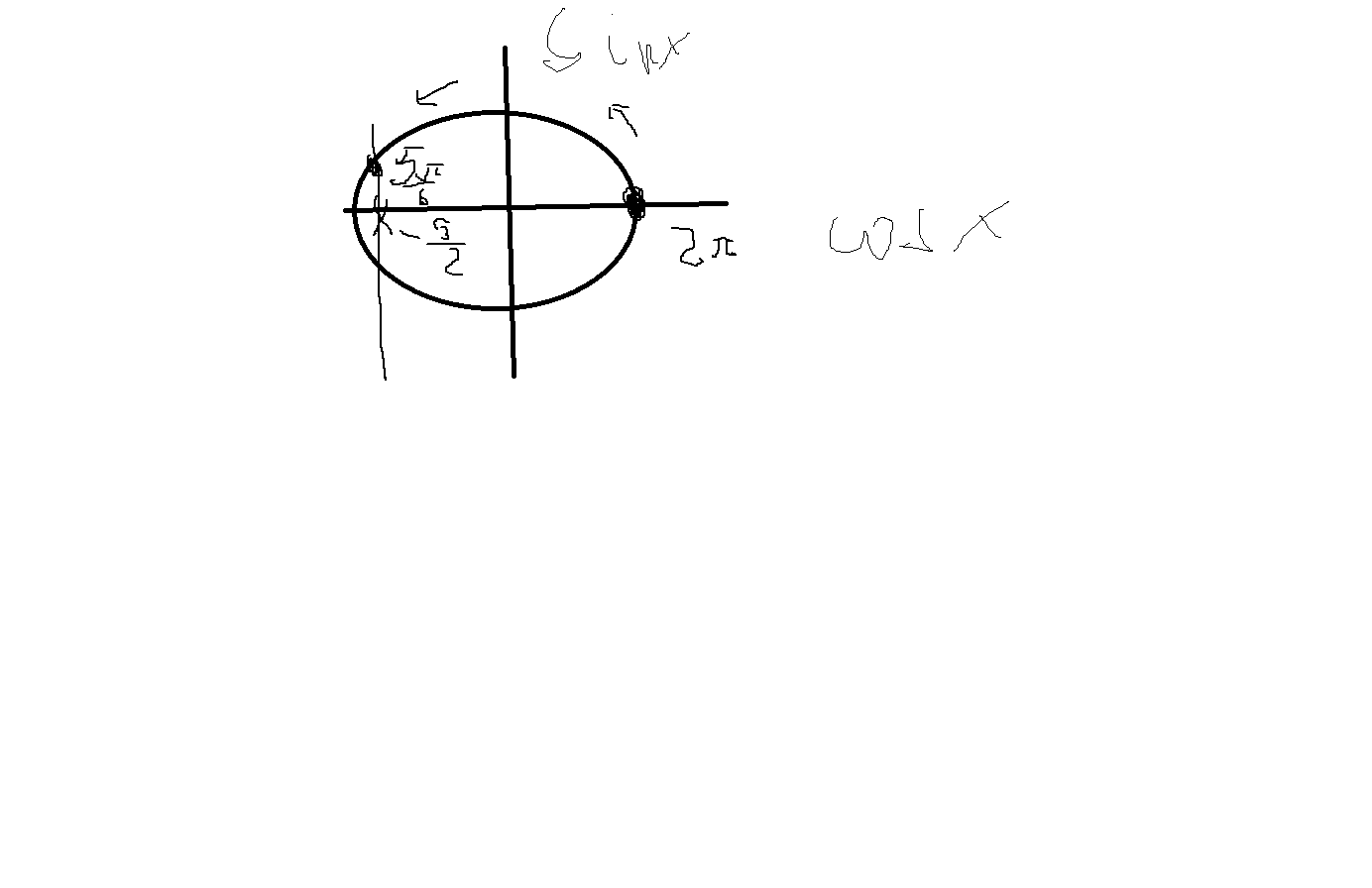
cos(17π/6)=сos(2*5/6*pi)=cos(2pi+5pi/6)=cos(-корен3/2) вот рисунок

Поскольку cos x является периодической функцией с периодом 2π, то через каждые 2π значание косинуса повторяется
Поэтому сначала выделим целую часть и количество 2π и спокойненько эти 2π убираем.
17π/6 = 3π - π/6 = 2π + π - π/6.
Итак, cos(17π/6) = cos(π - π/6) =
Испоьзуем формулы приведения. При вычитании из угла π острого угла π/6 получаем всё тот же косинус, т.е. cos(π - α) = cos α. Что в нашем случае соответствует cos(π - π/6) = ±cos π/6
Теперь определим знак cos(π - π/6) . Для этого найдём четверть, в которой расположен угол π -π/6. Очевидно, что это 2-я четверть. Известно, что в 2-ой четверти косинус отрицателен, поэтому
cos(π - π/6) = -cosπ/6 = -0,5 √3.