Диагонали прямоугольника пересекаются под углом 120. Сумма диагонали и меньшей стороны равна 36. Найдите диагональ прямоугольника

2 ответа

Посмотреть ответы

Megamozg

2205

Меньшая сторона против угла 60 проводим медиану она и высота и бессектриса. А диагонали делятся пополам. 2*d/2*sin30 +d=36 3/2D=36
d=24
Ответ:24

Хороший ответ

5 апреля 2023 01:28

DevAdmin

1720

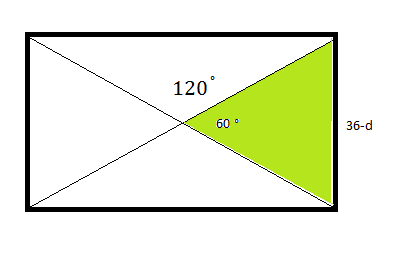
Пусть диагональ прямоугольника равна d, тогда меньшая сторона прямоугольника равна (36-d).
Тупой угол между диагоналями равен 120⁰, а острый угол равен 60⁰.
Из равнобедренного треугольника, образованного половинками диагоналей и меньшей стороной ( выделен на рисунке зеленым цветом) по теореме косинусов:
(36-d)²=(d/2)²+(d/2)²-2(d/2)(d/2) cos 60⁰ ⇒ (36-d)²=(d/2)²
или 36-d=d/2
36=3d/2
d=36·2/3
d=24

5 апреля 2023 01:28

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

угол при основании равнобедренного треугольника ABC равен 32 градусам, AB - его боковая сторона, AM - биссектриса треугольника. Найдите углы треугольн... Объем треугольной пирамиды равен 30. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, деля... Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2.Найдите высоту ромба.Помогите,пж,срочно надо.... Высота основания правильной треугольной призмы равна h, площадь ее боковой поверхности втрое больше площади основания. Найдите объем призмы... Какие утверждения верные? 1 Все диаметры окружности равны между собой. 2 Диагональ трапеции делит её на два равных треугольника. 3 Диагонали ромба...