Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
3 апреля 2023 01:28
1108
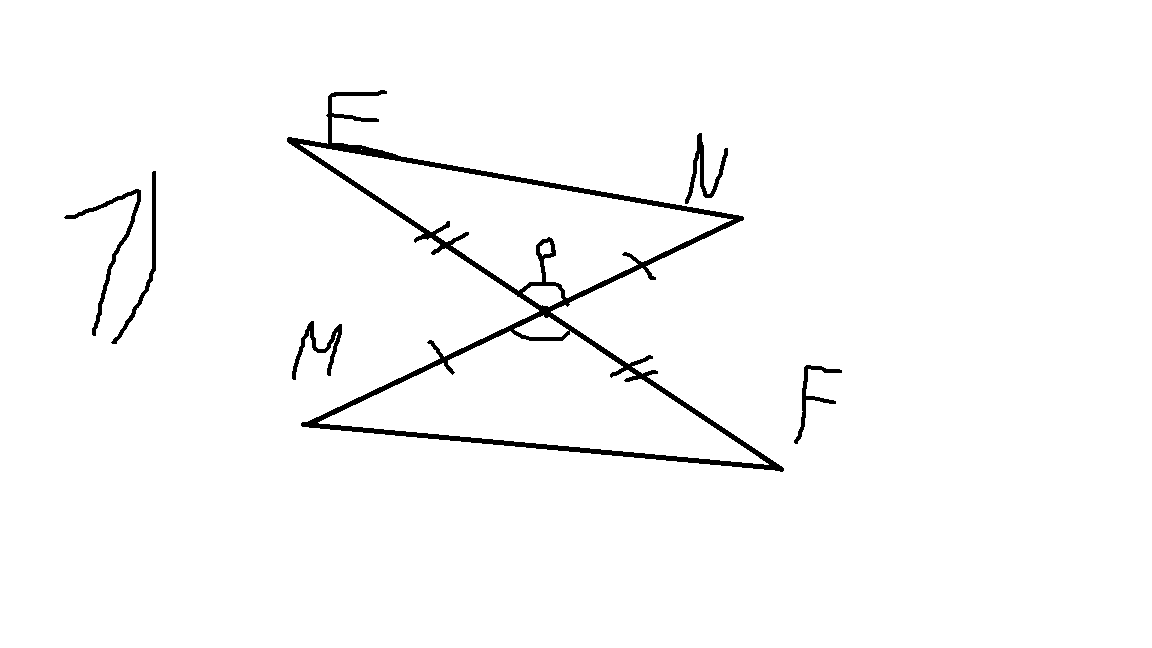
Помогите решить мы на карантине и нам задали Вариант2.1. Отрезки MN и EF пересекаются в их середине P. Докажите, что EN ││MF.
2. Отрезок AD - биссектриса ∆ ABC. Через точку D проведена прямая, параллельная стороне AB и пересекающая сторону AC в точке F. Найдите углы ∆ ADF, если ∠ BAC = 720.
1
ответ
1. Ну так как Р - середина, то ЕР=РF и МР=РN. Т. к. углы MPF и EPN вертикальны, они равны. А если EP=PF, MP=PN, и угол MPF равен углу EPN, то по 1-ому признаку равенства треугольников треугольник ENP и треугольник MPF равны, значит все их стороны и углы равны, тоесть и угол PMF равен углу PNE, а если так, то при секущей MN эти накрест-лежащие углы равны, значит по первому признаку EN II MF.
2. Только слушай УГОЛ BAC НЕ МОЖЕТ БЫТЬ 720 ГРАДУСОВ, Я ПОСТАВЛЮ В НЕГО НАВЕРНОЕ 120 ГРАДУСОВ. Т. к. AD - биссектриса следовательно угол BAD равен углу DAF что и равно 120:2=60 градусов каждый. Т. к. АВ II FD то по 2-ому свойству параллельных прямых BAF+AFD=180 градусов, значит угол AFD равен 180-60-60=60 градусов. Н уи т. к. сумма всех углов треугольника равна 180-ти градусам, то угол ADF равен 180-60-60=60 градусов.
2. Только слушай УГОЛ BAC НЕ МОЖЕТ БЫТЬ 720 ГРАДУСОВ, Я ПОСТАВЛЮ В НЕГО НАВЕРНОЕ 120 ГРАДУСОВ. Т. к. AD - биссектриса следовательно угол BAD равен углу DAF что и равно 120:2=60 градусов каждый. Т. к. АВ II FD то по 2-ому свойству параллельных прямых BAF+AFD=180 градусов, значит угол AFD равен 180-60-60=60 градусов. Н уи т. к. сумма всех углов треугольника равна 180-ти градусам, то угол ADF равен 180-60-60=60 градусов.
0
·
Хороший ответ
5 апреля 2023 01:28
Остались вопросы?
Еще вопросы по категории Геометрия
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна 15 дм. Чему равна гипотенуза?...
Хорды AB и CD пересекаются в точке F так, что BF =16см, AF=4см, CF=DF. найдите CD Пожалуйста срочно...
Используя рисунок, укажите верные утверждения 1) угол AKD И BKD - смежные углы. 2) угол BKD И BKE - вертикальные углы 3) угол AKE - тупой угол 4) у...
Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 120°. Высота цилиндра равна 5 см, радиус цилиндра – 2V3 см. Найти площад...
В треугольнике ABC известно,что AB=BC, угол ABC=106 градусов .Найдите угол BCA .Ответ дайте в градусах...