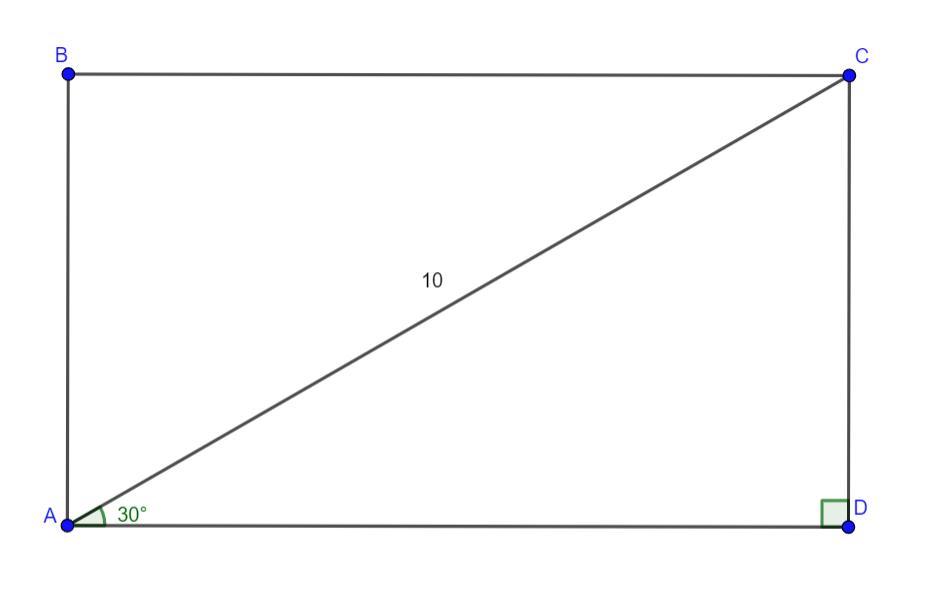
В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника, делённую на √3

1 ответ

Посмотреть ответы

d.scherbetov

Ответ:
25
Объяснение:
Дано:
ABCD - прямоугольник
AC = 10 - диагональ,
∠CAD = 30°
Найти: $\dfrac}{\sqrt 3}$
Решение:
$\displaystyle S_ = AD \cdot CD$
Рассмотрим ΔACD - прямоугольный, ∠ADC = 90°, AC - гипотенуза
∠CAD = 30° ⇒ CD = 5 (катет, противолежащий углу в 30°, равен половине гипотенузы)
Найдём AD по теореме Пифагора:
$\displaystyle AD^2 + CD^2 = AC^2 \\ \\ AD^2 = AC^2 - CD^2 \\ \\ AD^2 = 10^2 - 5^2 = 100 - 25 = 75 \\ \\ AD = \sqrt = \sqrt = 5 \sqrt 3$

Найдём площадь прямоугольника ABCD:
$\displaystyle S_ = AD \cdot CD = 5\sqrt 3 \cdot 5 = 25\sqrt 3 \\ \\ \frac }{\sqrt 3} = \frac{\sqrt 3} = 25$

Хороший ответ

1 сентября 2022 20:55

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

99 баллов!Дал бы больше но нельзя. Боковая поверхность правильной треугольной призмы 6 .Найдите высоту призмы , если прямая, проходящая через центр ве... ПОМОГИТЕ, ПОЖАЛУЙСТА 1.Около окружности описана трапеция, периметр которой равен 84. Найдите длину её средней линии. 2.Периметр =60. 3.Периметр =44.... В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 6.Найдите расстояние между точками A и С1... Докажите, что в равнобедренной трапеции углы при каждом основании равны.... 2. Найдите стороны равнобедренного треугольника, если его периметр равен 76 см, а основание на 14 14 см меньше боковой стороны....