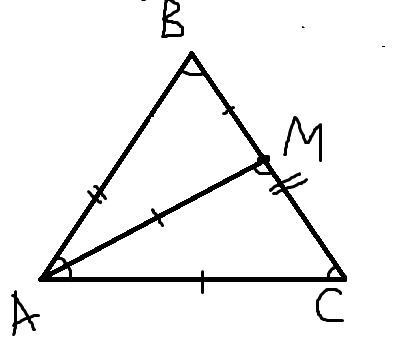
ДАЮ 50 баллов!! Геометрия, 7 класс. Мерзляк, Полонский Якир. Номер 404. Треугольник ABC равнобедренный с основанием AC. На стороне BC отметили точку M так, что BM=AM=AC. Найдите углы треугольника ABC.

1 ответ

Посмотреть ответы

DevAdmin

1720

Чертеж приложен.
Рассмотрим треугольник AMC - по условию он равнобедренный, AM = AC. Соответственно, ∠С = ∠СMA.
Рассмотрим треугольник AMB - он тоже равнобедренный (AM = BM). Соответственно, ∠B= ∠BAM, откуда ∠BMA = 180° - 2 ∠B.
Углы ∠CMA и ∠BMA - смежные, а значит их сумма равна 180°:
∠C + 180° - 2∠B = 180° ⇒ ∠C = 2∠B.
По условию треугольник АВС - равнобедренный, AB = BC, а значит ∠A = ∠C = 2∠B.
Сумма углов любого треугольника равна 180°:
∠A + ∠B + ∠C = 180°.
В итоге имеем линейное уравнение относительно ∠B:
2∠B + ∠B + 2∠B = 180°;
5 ∠B = 180°⇒ ∠B = 36°.
Тогда ∠А = ∠С = 2 · 36° = 72°.
ОТВЕТ: ∠A = ∠C = 72°, ∠B = 36°.

Хороший ответ

5 апреля 2023 05:11

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найдите радиус окружности вписанной в правильный шестиугольник со стороной 3 корня деленное на 2... Как начертить сумму неколлинеарных вектора... Обчислить: 1) 4 cos 90° + 2 cos 180° - tg 180°; 2) cos 0° - cos 180° + sin 90°.... Точка Н - ортоцентр труегольника Авс.Прямая АН пересекает описанную около АВС окружность в точке А1. Докажите,что прямая ВС делит отрезок НА1 пополам.... основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD=DM=a. найдите площадь поверхности пирамиды...