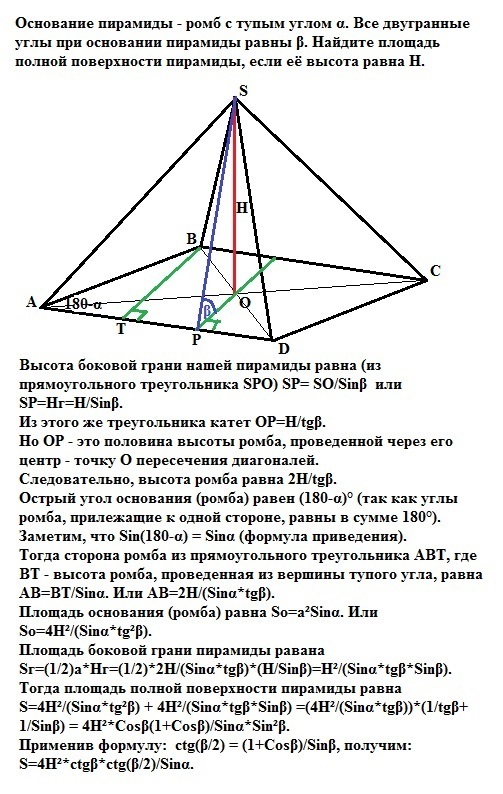
Основание пирамиды - ромб с тупым углом α. Все двугранные углы при основании пирамиды равны β. Найдите площать полной поверхности пирамиды, если её высота равна H. Буду очень благодарен тому, кто решит эту задачу.

Высота боковой грани нашей пирамиды равна (из прямоугольного треугольника SPO) SP= SO/Sinβ или
SP=H/Sinβ.
Из этого же треугольника катет ОР=Н/tgβ.
Но ОР - это половина высоты ромба, проведенной через его центр - точку О пересечения диагоналей.
Следовательно, высота ромба равна 2Н/tgβ.
Острый угол основания (ромба) равен (180-α)° (так как углы ромба, прилежащие к одной стороне, равны в сумме 180°).
Заметим, что Sin(180-α) = Sinα (формула приведения).
Тогда сторона ромба из прямоугольного треугольника АВТ, где ВТ - высота ромба, проведенная из вершины тупого угла), равна АВ=ВТ/Sinα. Или АВ=2Н/(Sinα*tgβ).
Площадь основания (ромба) равна So=а²Sinα. Или
So=4Н²/(Sinα*tg²β).
Площадь боковой грани пирамиды равана
Sг=(1/2)a*Hг=(1/2)*2Н/(Sinα*tgβ)*(H/Sinβ)=Н²/(Sinα*tgβ*Sinβ).
Тогда площадь полной поверхности пирамиды равна
S=4Н²/(Sinα*tg²β) + 4Н²/(Sinα*tgβ*Sinβ) =(4Н²/(Sinα*tgβ))*(1/tgβ+1/Sinβ) = 4Н²*Cosβ(1+Cosβ)/Sinα*Sin²β.
Применив формулу ctg(β/2) = (1+Cosβ)/Sinβ, получим:
S=4Н²*ctgβ*ctg(β/2)/Sinα.