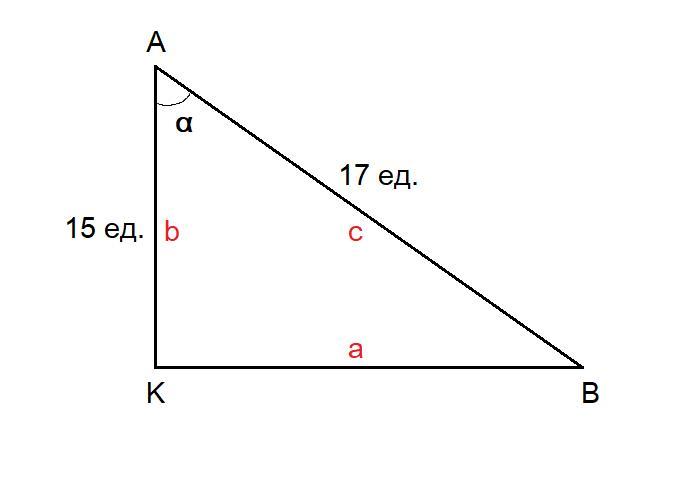
В прямоугольном треугольнике ABK гипотенуза AB равна 17, катет AK равен 15. Найдите тангенс угла А ( 8 класс )

1 ответ

Посмотреть ответы

y.visockiy

Дано: $\sf \triangle ABK$ - прямоугольный, $\sf AB$ - гипотенуза, $\sf AK$ - катет.
$\sf AB = 17$ ед., $\sf AK = 15$ ед.
Найти: $\bf tg (\angle A) - ?$
------------------------------------------------------------------------------------------
Решение:
В прямоугольном $\sf \triangle ABK$ - $\sf \angle A$ острый.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
$\sf \Rightarrow tg (\angle A)=\dfrac$
Найдём катет $\sf KB$ по теореме Пифагора:
$\boxed{\sf a=\sqrt{^-^}}$ , где $\sf a$ и $\sf b$ - катеты, $\sf c$ - гипотенуза.
$\sf \Rightarrow KB = \sqrt=\sqrt=\sqrt=\sqrt=8$ ед.
Зная величину обоих катетов, найдём тангенс $\sf \angle A$ :
$\bold{\Rightarrow tg (\angle A) = \dfrac=\dfrac}$
Ответ: $\boxed{\bf tg(\angle A)=\dfrac}}$

Хороший ответ

14 октября 2022 16:38

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Основание трапеции - 44 и 16 см, а боковые стороны - 17 и 25 см. Найти высоту трапеции.... Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30 градусов. Боковая сторона треугольника равна 4. Найдите площадь этог... Докажите, что в треугольнике медиана не меньше высоты, проведенной из той же вершины... В прямоугольнике ABCD диагонали пересекаются в точке O.E-середина стороны AB,угол BAC=50градусов.Чему равен угол EOD... Что такое пифагоровы штаны...