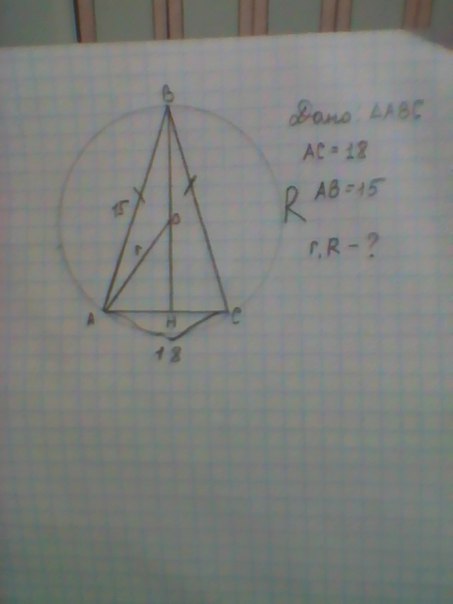
Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиус вписанной в треугольник и описанной около треугольника окружности. Рисунок прилагается

1 ответ

Посмотреть ответы

v.petrogradov

Радиус описанной окружности: R=abc/4S.
Радиус вписанной окружности: r=S/p.
p=(a+b+c)/2=(15+15+18)/2=24 см
Площадь тр-ка по ф-ле Герона:
S=√(24(24-15)(24-15)(24-18))=108 cм².
R=15·15·18/(4·108)=9.375 см.
r=108/24=4.5 см.

Хороший ответ

14 октября 2022 17:09

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Чему равна градусная мера дуги ASE? 2 угла AOE? Угол AOE? 1/2 AOE? 1/4 AOE?... Окружность с центром в точке О описана около равнобедренного треугольника АВС , в котором АВ=ВС и угол АВС=88 градусов. Найдите величину угла ВОС. Отв... Площадь большого круга шара равна 3.найдите площадь поверхности шара... Диагонали параллелограмма равны 8 см и 10 см а угол между ними 30 градусов.Найти стороны параллелограмма... Прямые CD и AB пересекаются в точке 0. Известно, что в треугольниках AOC и BOD угл ACO = углу BD0, AC = 10, AO = 12, BD = 20, OD = 16. Найди ОС, ОВ.по...