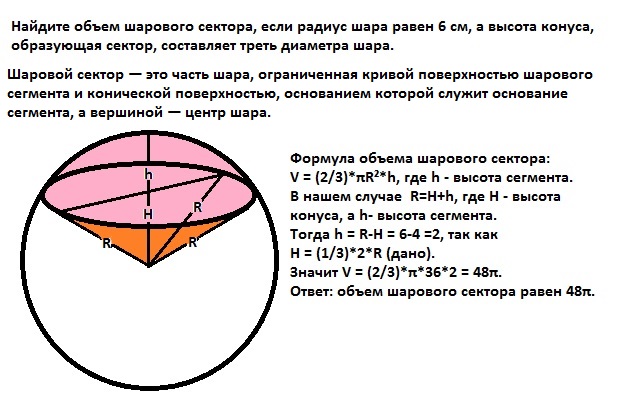
Найдите объем шарового сектора, если радиус шара равен 6 см, а высота конуса, образующая сектор, составляет треть диаметра шара.

1 ответ

Посмотреть ответы

v.petrogradov

Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной — центр шара.
Формула объема шарового сектора:
V = (2/3)*πR²*h, где h - высота сегмента.
В нашем случае R=H+h, где Н - высота конуса, а h- высота сегмента.
Тогда h = R-H = 6-4 =2, так как
Н = (1/3)*2*R (дано).
Значит V = (2/3)*π*36*2 = 48π.
Ответ: объем шарового сектора равен 48π.

Хороший ответ

14 октября 2022 17:24

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Сторона основания правильной треугольной пирамиды равна 6, а её боковое ребро образует с плоскостью основания угол 45. Найти объём пирамиды... Угол, противолежащий основанию равнобедренного треугольника равен 120 градусам, боковая сторона треугольника равна 8 см. Найдите диаметр окружности оп... Помогите пожалуйста =) Окружность задана уравнением (x+1)^2+(y-2)^2=16 а)укажите координаты центра и радиус окружности б)Принадлежат ли данной окружно... Найти объем правильной шестиугольной призмы, все ребра которой равны 10.... В правильной треугольной пирамиде сторона основания равна 2корень из 3, а высота 2 см.. Найти угол наклона бокового ребра к плоскости основания. Ответ...