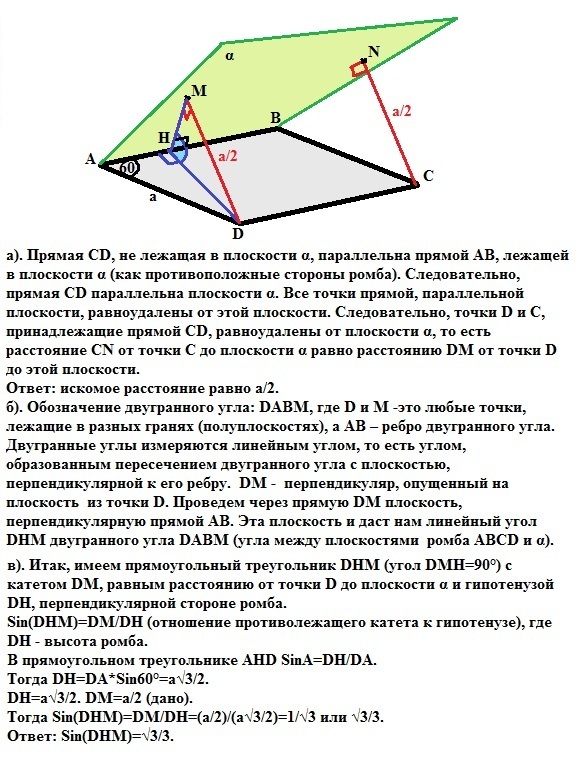
Помогите пожалуйста с этой геометрией)))))) Сторона AB ромба ABCD равна а,один из углов равен 60 градусов.Через сторону AB проведена плоскость альфа на расстоянии a/2 от точки D.
а)найти расстояние от точки C до плоскости альфа.
б)покажите на рисунке линейный угол двугранного угла DABM. M принадлежит альфа.
в)Найдите синус угла между плоскостью ромба и плоскостью альфа. PS:если можно с чертежом))))

A). Теорема: Если прямая, не лежащая в данной плоскости,
параллельна какой-нибудь прямой, лежащей в этой плоскости, то
она параллельна самой плоскости. В нашем случае прямая CD, не
лежащая в плоскости α, параллельна прямой АВ, лежащей в
плоскости α (как противоположные стороны ромба). Следовательно,
прямая CD параллельна плоскости α.
Все точки прямой, параллельной плоскости, равноудалены от этой плоскости. Следовательно, точки D и С, принадлежащие прямой СD, параллельной плоскости α, равноудалены от плоскости α, то есть расстояние СN от точки С
до плоскости α равно расстоянию DM от точки D до этой плоскости.
Ответ: искомое расстояние равно а/2.

б). Определение: Полуплоскости, образующие двугранный угол,
называются гранями двугранного угла. Общая для граней прямая АВ
(линия пересечения плоскостей) называется ребром двугранного
угла. Обозначение двугранного угла: DABМ, где D и M -это любые
точки, лежащие в разных гранях, а АВ – ребро двугранного угла.
Двугранные углы измеряются линейным углом, то есть углом,
образованным пересечением двугранного угла с плоскостью,
перпендикулярной к его ребру.
Расстояние от точки D до плоскости α равно длине перпендикуляра
DМ, опущенного на плоскость из этой точки. Проведем через
прямую DМ плоскость, перпендикулярную прямой АВ. Эта плоскость и
даст нам линейный угол DHM двугранного угла DABМ (угла между
плоскостями ромба АВСD и α).

в). Итак, имеем прямоугольный треугольник DHM (угол DMH=90°) с
катетом DM, равным расстоянию от точки D до плоскости α и
гипотенузой DH, перпендикулярной стороне ромба.
Sin(DHM)=DM/DH (отношение противолежащего катета к гипотенузе),
где DH - высота ромба.
В прямоугольном треугольнике АНD SinA=DH/DA.
Тогда DH=DA*Sin60°=a√3/2.
DH=a√3/2. DM=a/2 (дано).
Тогда Sin(DHM)=DM/DH=(a/2)/(a√3/2)=1/√3 или √3/3.
Ответ: Sin(DHM)=√3/3.