Помогите решить(√x+1)-(√9-x)=(√2x-12). На скрине то уравнение, которое должно быть

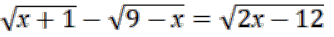
1) Так как выражения под знаком корня не могут быть отрицательными, то x+1>=0, 9-x>=0, 2*x-12>=0. Отсюда x>=-1, x<=9, x>=6. Окончательно область допустимых значений (ОДЗ) переменной x задаётся неравенством 6<=x<=9.

2) Возводя обе части в квадрат, получаем уравнение x+1-2*sqrt[(x+1)*(9-x)]+9-x=2*x-12, где sqrt[ ] - квадратный корень из выражения, находящегося в скобках [ ]. Это уравнение приводится к виду 2*sqrt[(x+1)*(9-x)]=22-2*x, или sqrt[(x+1)*(9-x)]=11-x. Возводя обе части в квадрат, получаем: (x+1)*(9-x)=(11-x)^2, или x^2-15*x+56=0. Отсюда x1=8, x2=7. Оба значения принадлежат ОДЗ. Подставляя их в исходное уравнение, убеждаемся, что они ему удовлетворяют. Ответ: x1=8, x2=7.