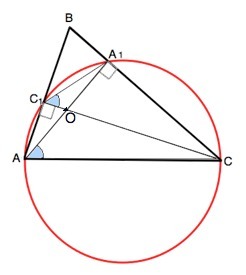
В остроугольном треугольнике ABC проведены высоты АА1 и CC1 Докажите, что углы СС1А1 и САА1 равны.

Способ 1.
В ∆ АВС высоты АА1 и СС1 со сторонами два прямоугольных треугольника АС1С и АА1С с общей гипотенузой АС.
Следовательно, вокруг них можно описать окружность с диаметром АС, на который опираются прямые углы АС1С и АА1С.
Вписанные углы А1АС и А1С1С опираются на одну дугу А1С. Вписанные углы, опирающиеся на одну дуга, равны. ⇒
∠СС1А1=∠САА1. Доказано. ---------
Способ 2.
Рассмотрим ∆ АОС1 и А1ОС.
Эти треугольники подобны по двум углам - прямому при С1 и А1 и вертикальному при точке пересечения высот О.
Из подобия следует пропорциональность сторон:
С1О:А1О=АО:СО,
откуда имеем пропорциональность тех же сторон в ∆ АОС и ∆ А1ОС1.
Вертикальные углы при вершине О этих треугольников равны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Следовательно, углы СС1А1 и САА1 равны. Доказано.