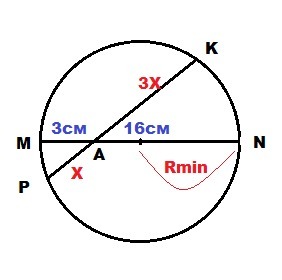
хорды MN и PK пересекаются в точке A так, что MA= 3 см, NA= 16м, PA : KA= 1 : 3. Найдите PK и наименьшее значение радиуса этой окружности.

1 ответ

Посмотреть ответы

DevAdmin

1690

$\dfrac =\dfrac$ ⇒ KA = 3PA

По свойству пересекающихся хорд :
PA * KA = NA * MA
PA * 3PA = 16 * 3
PA² = 16 ⇒ PA = 4 см
KA = 3PA = 3*4 = 12 см
PK = PA + KA = 4+12 = 16 см

Самая большая хорда в любой окружности - это диаметр. Поэтому диаметр не может быть меньше любой из хорд, проведенных в окружности.
В данной окружности проведено 2 хорды :
MN = MA + NA = 3 + 16 = 19 см
PK = 16 см
Значит, наименьшее значение диаметра не может быть меньше 19 см.
Тогда наименьший радиус равен 19 : 2 = 9,5 см

Ответ: РК = 16 см; наименьший радиус 9,5 см

Хороший ответ

2 декабря 2022 04:19

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найдите угол ABD1 прямоугольного параллелепипеда, для которого , AB=5, AD=4, AA1=3 . Ответ дайте в градусах.... Найдите площадь трапеции ABCD. Размер каждой клетки 1 см х 1 см. Ответ дайте в квадратных сантиметрах.... номер 1:В параллелограмме ABCD AB = 7cм, AD= 12см. Биссектриса угла А пересекает сторону BC в точке Е. номер 2: На основании равнобедренного треуго... Площадь боковой поверхности правильной четырехугольной призмы равна Q.Сечение призмы,проходящее через диагональ нижнего основания и противолезащую вер... Имеется торт в виде четырехугольной призмы с размерами 80x80x120 см. Сколько крема потребуется чтобы обмазать торт, если на 1 см2 уходит 50 грамм крем...