В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания равна 10,5. Найдите высоту пирамиды.

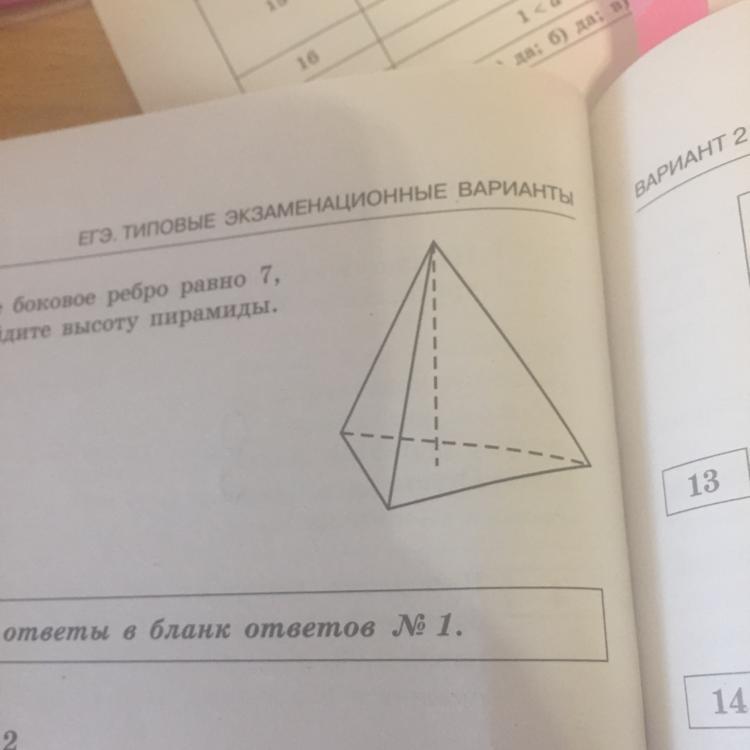
1 ответ

Посмотреть ответы

DevAdmin

1720

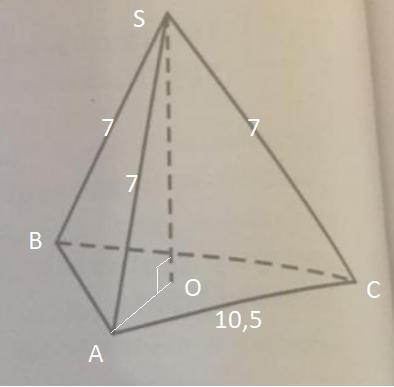
Дано : SABC - правильная треугольная пирамида,
SA = SB = SC = 7; AB = AC = BC = 10,5
Найти : SO
Решение :
Так как боковые рёбра равны, то высота пирамиды опускается в центр окружности, описанной около основания пирамиды, то есть
OA = OB = OC = R - радиус окружности, описанной около ΔABC.
Пирамида правильная, значит, в основании лежит равносторонний треугольник ABC. Тогда радиус описанной окружности
$R = \dfrac a{\sqrt3}\ \ \ \Rightarrow \ \ \ OA=\dfrac{\sqrt 3}=\dfrac{\sqrt 3}=3,5\sqrt3$
SO⊥(ABC) ⇒ ΔSOA - прямоугольный
Теорема Пифагора
$SO^2=SA^2-OA^2=7^2-(3,5\sqrt3)^2=\\\\~~~=(3,5\cdot2)^2-3,5^2\cdot \sqrt3^2=3,5^2\cdot(4-3)=3,5^2\\\\\boldsymbol$
Ответ : 3,5

Хороший ответ

2 декабря 2022 04:58

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Катеты равнобедренного прямоугольного треугольника равны   Найдите радиус окружности, вписанной в этот треуголь... Как называется угол 360 градусов если 180градусов называется развернутый... Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника,если его периметр равен 77 см....... Найдите координаты вершины B параллелограмма ABCD, если A (3; −2), C (9; 8), D (−4; −5).... Любой ромб является а квадратом б прямоугольником в параллелограмом нет правельного ответа...