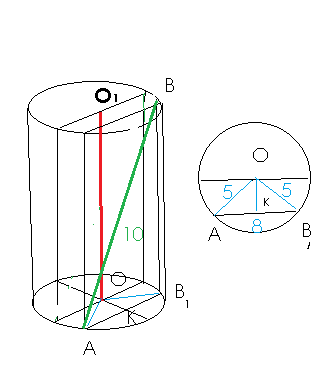
Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус основания равен 5 см, высота цилиндра равна 6 см, АВ=10 см. Определите расстояние между прямой АВ и осью цилиндра.

1 ответ

Посмотреть ответы

Megamozg

2205

Проводим ВВ₁ || OO₁
Треугольник АВВ₁ - прямоугольный
АВ₁=8 ( по теореме Пифагора) или потому то это египетский треугольник
АВ₁²=АВ²-ВВ₁²=10²-6²=64=8²
Рассмотрим треугольник АОВ₁ ( см рисунок справа)
Равнобедренный треугольник. проведем высоту ОК. По теореме Пифагора
ОК=3.
Или потому что треугольник АОК - египетский
ОК- расстояние между плоскостью, содержащей отрезок АВ и плоскостью, содержащей ось ОО₁

Хороший ответ

2 декабря 2022 05:01

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найдите синус угла C. В ответе укажите значение синуса, умноженное на √29.... Найдите tg α, если sin α=3/5 и 90<α<180. Напишите, пожалуйста, полное решение и объяснение к нему.... Найдите стороны прямоугольного треугольника , в котором: а) гипотенуза равна 10 см, разность катетов - 2 см; б) гипотенуза равна 26 см, а отношение ка... На стороне AC треугольника ABC выбрана точка D так, что DC=2AD, точка М-середина AB, точка N- середина стороны BD; MN=6см, ∠BDC=1400. Найдите дли... В прямоугольном треугольнике АВК гипотенуза АВ равна 13, катет ВК равен 5. Найдите косинус угла А....