Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
30 ноября 2022 06:24
1508
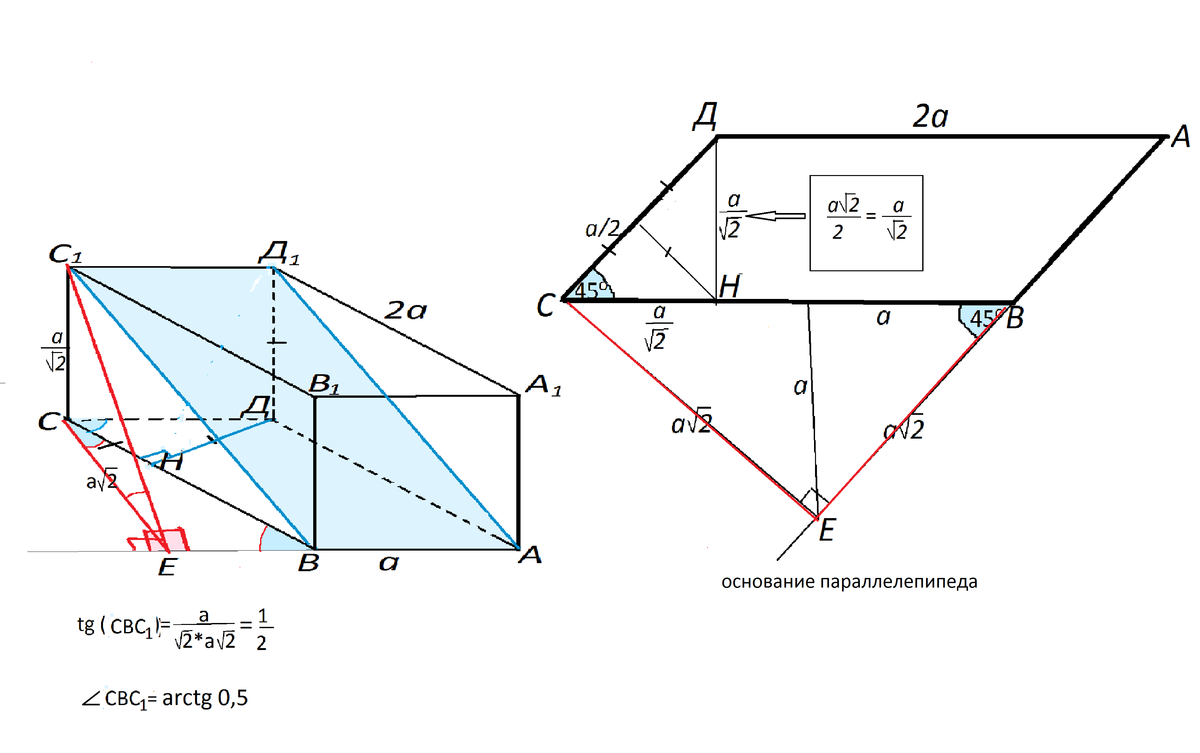
Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны а и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите: а) меньшую высоту параллелограмма; б) угол между плоскостью АВС1 и плоскостью основания; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда.
1
ответ
Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁ является
параллелограмм ABCD, стороны которого равны а и 2а, острый
угол равен 45°. Высота параллелепипеда равна меньшей высоте
параллелограмма. Найдите:
а) меньшую высоту параллелограмма;
б) угол между плоскостью АВС₁ и плоскостью основания;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
--------
Пусть в параллелограмме ABCD, стороны которого равны а и 2а,
сторона АВ=СD=а и
ВС=АD=2а
1) меньшая высота параллелограмма идет из вершины тупого угла
D к большей стороне ВС и отрезает от него равнобедренный
прямоугольный треугольник с катетами
DН=СН=СD*sin(45°)=(а√2):2=а/√2
Найдя меньшую высоту основания, мы нашли высоту
параллелепипеда, равную ей по условию.
СС₁=DН=а/√2
2) Угол между плоскостью АВС1 и плоскостью основания:
. Проведем из С1 перпендикуляр к продолжению АВ и точку пересечения обозначим Е.
По теореме о 3-х перпендикулярах
С₁Е ⊥ АЕ.
Угол СЕC₁ - искомый.
Так как тупой угол параллелограмма ABCD равен 180°-45°=135°,
∠ СВЕ=45° ( еще и потому, что эти углы накрестлежащие при пересечении параллельных СD и ВА секущей СВ).
Отсюда
СЕ=ВЕ=СВ*sin(45°)=2а*(√2):2=а√2
tg ∠CЕC₁=СС₁:СЕ=а/√2):(а√2)=1/2
∠ СЕC₁=arctg 1/2 ,
3) Площадь боковой поверхности параллелепипеда равна произведению его высоты на периметр основания.
Sбок=2*(а+2а)*СС1=6а*а/√2=3а²√2
4) Площадь поверхности параллелепипеда равна сумме площади боковой поверхности и удвоенной площади основания ( т.к. оснований два).
Удвоенная площадь основания
2S осн=2*BC*СD*sin(45°) =2*2a*а*(√2):2=4a²(√2):2= 2a²√2
Sполн=3а²√2+2a²√2=5а²√2
---
[email protected]
параллелограмм ABCD, стороны которого равны а и 2а, острый
угол равен 45°. Высота параллелепипеда равна меньшей высоте
параллелограмма. Найдите:
а) меньшую высоту параллелограмма;
б) угол между плоскостью АВС₁ и плоскостью основания;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
--------
Пусть в параллелограмме ABCD, стороны которого равны а и 2а,
сторона АВ=СD=а и
ВС=АD=2а
1) меньшая высота параллелограмма идет из вершины тупого угла
D к большей стороне ВС и отрезает от него равнобедренный
прямоугольный треугольник с катетами
DН=СН=СD*sin(45°)=(а√2):2=а/√2
Найдя меньшую высоту основания, мы нашли высоту
параллелепипеда, равную ей по условию.
СС₁=DН=а/√2
2) Угол между плоскостью АВС1 и плоскостью основания:
. Проведем из С1 перпендикуляр к продолжению АВ и точку пересечения обозначим Е.
По теореме о 3-х перпендикулярах
С₁Е ⊥ АЕ.
Угол СЕC₁ - искомый.
Так как тупой угол параллелограмма ABCD равен 180°-45°=135°,
∠ СВЕ=45° ( еще и потому, что эти углы накрестлежащие при пересечении параллельных СD и ВА секущей СВ).
Отсюда
СЕ=ВЕ=СВ*sin(45°)=2а*(√2):2=а√2
tg ∠CЕC₁=СС₁:СЕ=а/√2):(а√2)=1/2
∠ СЕC₁=arctg 1/2 ,
3) Площадь боковой поверхности параллелепипеда равна произведению его высоты на периметр основания.
Sбок=2*(а+2а)*СС1=6а*а/√2=3а²√2
4) Площадь поверхности параллелепипеда равна сумме площади боковой поверхности и удвоенной площади основания ( т.к. оснований два).
Удвоенная площадь основания
2S осн=2*BC*СD*sin(45°) =2*2a*а*(√2):2=4a²(√2):2= 2a²√2
Sполн=3а²√2+2a²√2=5а²√2
---
[email protected]
0
·
Хороший ответ
2 декабря 2022 06:24
Остались вопросы?
Еще вопросы по категории Геометрия
Чему равна ордината центра окружности, заданной уравнением ( x +2)^2 +( y −3)^2 =25? ...
В треугольнике ABC AC=BC, sinACD=2/√5, AH и CD высоты. Найдите tgBAH...
равнобедренного триугольника 30см боковая стороно 13см найдите основную сторону триугольника...
отрезки KL и MN пересекаются в точке O которая является серединой отрезка KL известно что угол MKL = углуNLK. найдите отношение MO: ON...
Сторона основания правильной четырехугольной пирамиды равна 10 см. Высота пирамиды равна 12см. Найдите апофему. НУЖНО С ДАНО И РЕШЕНИЕМ ОЧЕНЬ СРОЧНОО...