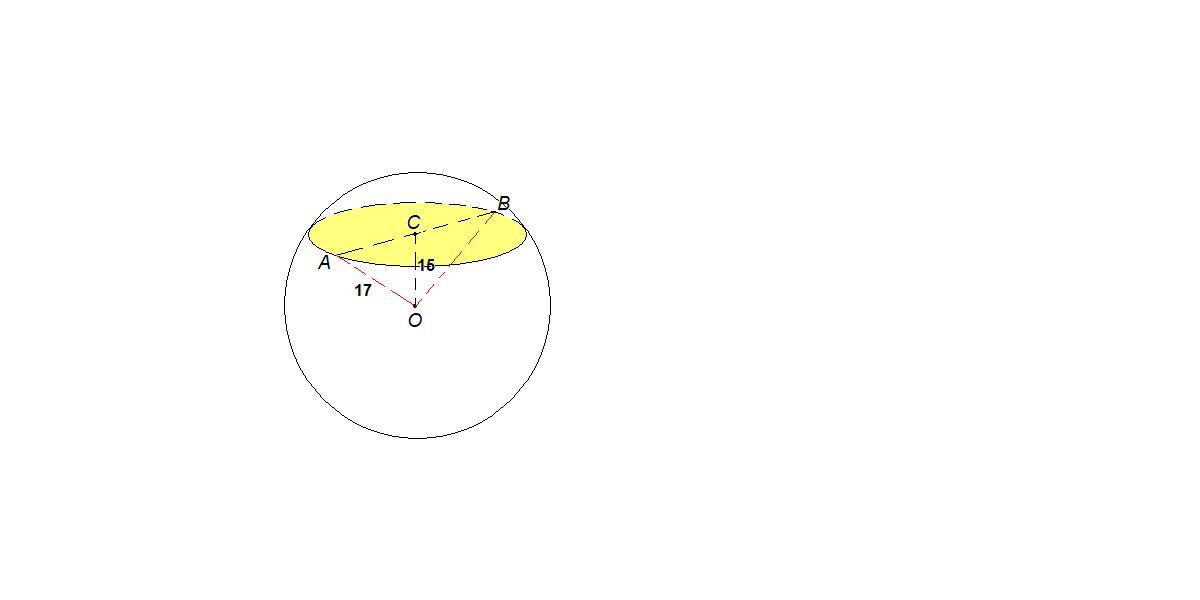
1) Радиус шара равен 17 см. Найдите площадь сечения шара, удалённого от его центра на 15 см.

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ: 64π см²

Объяснение:
Сечение шара - круг.
О - центр шара, С - центр сечения.
Отрезок, соединяющий центр шара с центром сечения, перпендикулярен плоскости сечения, поэтому
ОС = 15 см - расстояние от центра шара до сечения.
ОА = 17 см - радиус шара.
ΔАОС: ∠АСО = 90°, по теореме Пифагора
АС = √(ОА² - ОС²) = √(17² - 15²) = √(289 - 225) = √64 = 8 см
Площадь сечения:
S = πr², где r = АС - радиус сечения.
S = π · 8² = 64π см²

Хороший ответ

2 декабря 2022 07:01

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

1)В равнобедренном треугольнике угол при основании на 15 градусов меньше,чем при вершине,противоположной основанию.Найдите углы этого треугольника. 2)... Через прямую и не лежащую на ней точку можно провести плоскость, притом только одну... В треугольнике ABC известно , что ∠A=70° , ∠B=50°. Биссектриса ∠A пересекает сторону BC в точке M . Найдите угол AMC.... Через вершины A и C треугольника ABC, площадь которого равна 10 корней из 3 проведена окружность, пересекающая сторону AB в точке M, а продолжение сто... Найдите периметр участка земли прямоугольной формы, площадь которого равна 3200 м^2, а одна сторона в 2 раза больше другой. Ответ дайте в метрах. Помо...