Найдите площадь ромба, если его высота равна 2, а острый угол равен 30 градусов.

Ответ:
8
Объяснение:
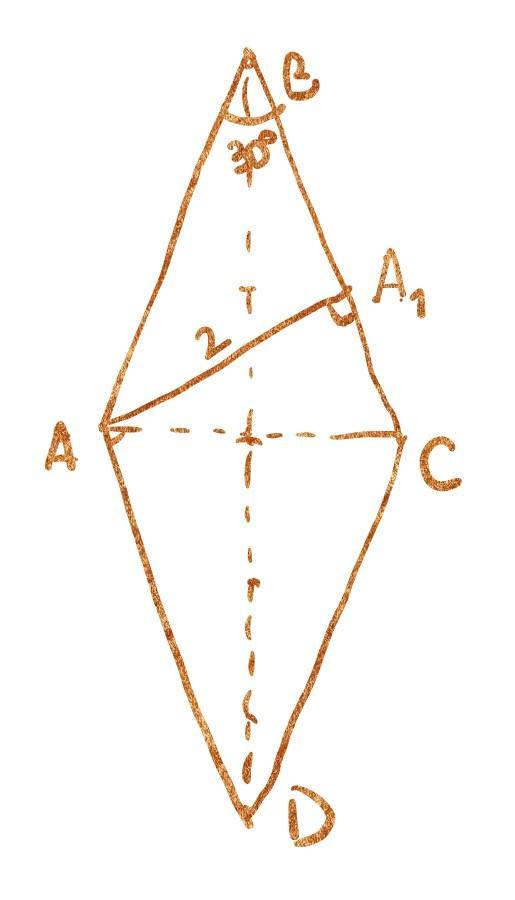
из треугольника ABA₁ (∠A₁ = 90°) AA₁ = 1/2 AB (как катет, лежащий против ∠ 30°) ⇒ AB = 2 · 2 = 4
S = BC · AA₁ = AB · AA₁ = 4 · 2 = 8

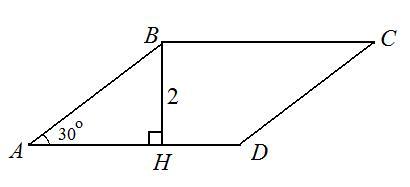
См. рисунок
Пусть дан ромб АВСD, ВН ⊥ АD, ВН = 2, ∠ВАD = 30°. Найдем площадь ромба.
Т.к. ромб - это параллелограмм, у которого все стороны равны, то АВ = ВС = СD = АD и поэтому площадь ромба можно найти по формуле
S = ah, где a - сторона параллелограмма, h - высота параллелограмма, проведенная к этой стороне.
Значит, нужно найти сторону ромба. Для этого рассмотрим прямоугольный ΔАВН (ВН - высота, ∠ВАН = 30°). ВН - катет, лежащий против угла в 30°, а, значит, он равен половине гипотенузы, т.е. гипотенуза АВ = 2ВН = 4.
Таким образом, площадь ромба можно вычислить так:
S = АD · ВН = АВ · ВН = 4 · 2 = 8.
Ответ: 8.