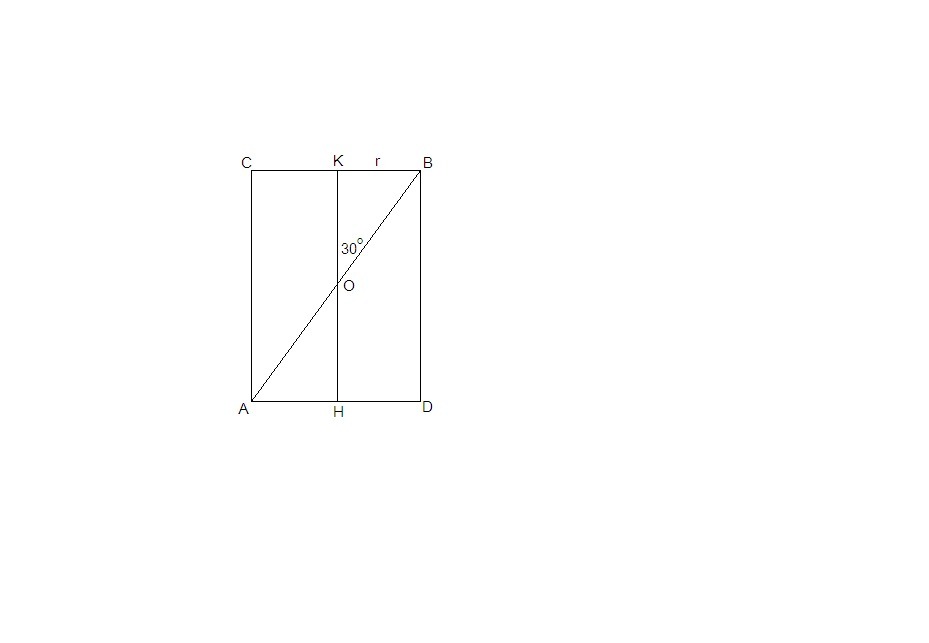
Отрезок АВ, концы которого лежат на арзных окружностях оснований цилиндра, пересекает ось цилиндра под углом 30 градусов. Найти объем цилиндра, если отрезок АВ = 4 корня из 3

1 ответ

Посмотреть ответы

DevAdmin

1720

Т.к. отрезок АВ пересекает ось цилиндра, они лежат в одной плоскости. Осевое сечение цилиндра на рисунке.
ΔКОВ = ΔНОА по катету и прилежащему острому углу (KB = AH = r, ∠КОВ = ∠НОА как вертикальные) ⇒ КО = ОН, АО = ОВ = АВ/2 = 2√3
ΔКОВ:
∠ОКВ = 90°, КВ = ОВ/2 = √3 как катет, лежащий напротив угла в 30°.
r = √3
ОК = ОВ·cos30° = 2√3·√3/2= 3 ⇒ KH = 6
h = 6 высота цилиндра
V = Sосн · h = πr²·h = π · 3 · 6 = 18π

Хороший ответ

16 декабря 2022 18:29

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

1)Докажите, что углы при основании равнобедренного треугольника равны. 2) Объясните, какой отрезок называется перпендикуляром, проведённым из данной т... угол при вершине,противолежащей основанию равнобедренного треугольника,равен 30 градусов. боковая сторона треугольника равна 22. найдите площадь этого... Площадь наибольшего диагонального сечения правильной шестиугольной призмы равна 10. Найдите площадь боковой поверхности этой призмы.... Даны координаты вершин четырехугольника ABCD: A(-6;1), B(0;5), C(6;-4),D(0,-8). Докажите, что это прямоугольник и найдите координаты точки пересечения... Основанием пирамиды является прямоугольник, диагональ которого равна d, и образует со сторон угол альфа. Высота пирамиды равна h. Найти объём пирамиды...