сформулировать определение средней линии трапеции. Докозать свойство средней линии трапеции. помогите ссрочно плиз

Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.
Свойства средней линии трапеции:
Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство:
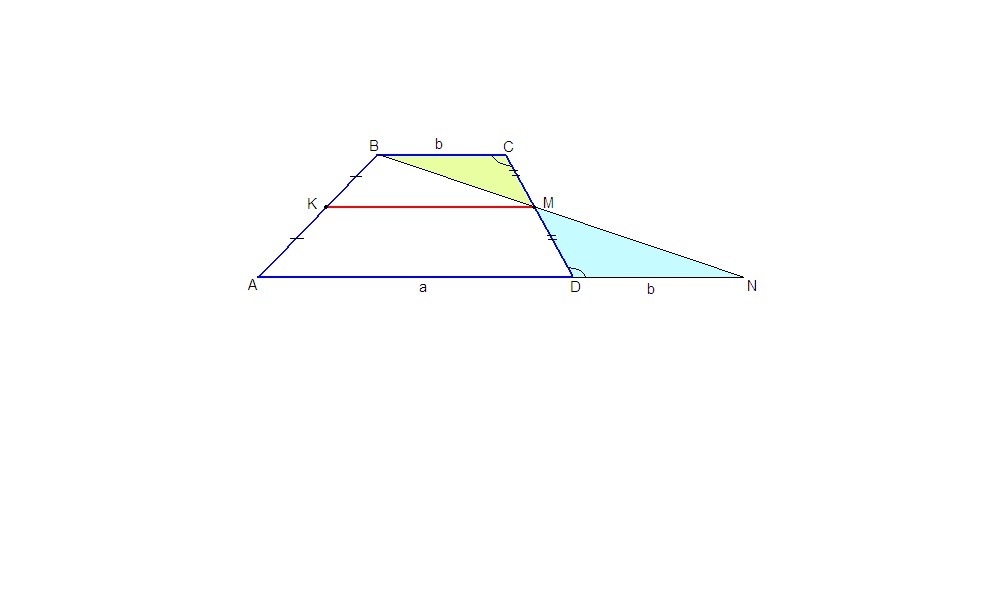
К и М - середины боковых сторон трапеции ABCD, КМ - ее средняя линия.

Проведем прямую ВМ.
ВМ ∩ AD = N.

CM = MD по условию,
∠BCМ = ∠NDM как накрест лежащие при пересечении параллельных AN и ВС секущей CD,
∠BMC = ∠NMD как вертикальные, ⇒
ΔBMC = ΔNMD по стороне и двум прилежащим к ней углам.

Значит, ВМ = MN, то есть КМ - средняя линия треугольника ABN, следовательно КМ║AN, а значит и КМ║AD.

Из равенства треугольников следует, что
DN = BC = b, значит AN = AD + BC = a + b,
а KM = AN/2 = (a + b)/2 как средняя линия треугольника ABN.