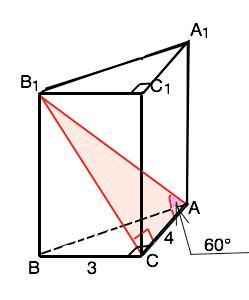
в основании прямой призмы авса1в1с1 лежит прямоугольный треугольник авс, угол с=90 гр, ас=4, вс=3, через ас и вершину в1 проведена плоскость, угол в1ас=60 гр. найдите площадь боковой поверхности призмы Помоогите

Ответ: 12√39 (ед. площади)
Объяснение:
Прямоугольный треугольник с катетами 3 и 4 - египетский, его гипотенуза 5 ( проверьте по т.Пифагора).
Проекция ВС наклонной В1С перпендикулярна СА. По т. о 3-х перпендикулярах В1С⊥СА. Треугольник В1СА - прямоугольный с углом В1АС=60°. В1С=АС•tg60°=4√3. Т.к. призма прямая, боковые ребра перпендикулярны основаниям, поэтому треугольник В1ВС прямоугольный. По т. Пифагора В1В=√(B1C²-BC²)=√[(4√3)²-3²]=√39
Боковое ребро прямой призмы является её высотой, а её боковые грани - прямоугольники.
Площадь боковой поверхности призмы находят умножением её высоты на периметр основания.
S(бок)=В1В•(АВ+ВС+АС)=√39•12=12√39 (ед. площади)