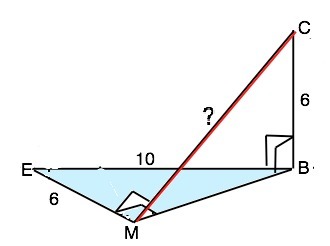
Прямоугольный треугольник MBE (∢M=90°) находится в плоскости α. BE=10 см, а ME=6 см. К этой плоскости проведён перпендикуляр CB длиной 6 см.Вычисли расстояние от точки C до стороны треугольника ME.
Плиз, объясните :3

1 ответ

Посмотреть ответы

Megamozg

2200

Отношение катета МЕ и гипотенузы ВЕ=3:5, значит, второй катет⊿ МВЕ (египетского) равен 8 см (и по т.Пифагора ВМ=8 см). По условию ВС - перпендикуляр к плоскости треугольника, следовательно, перпендикулярен ВЕ и ВМ. Расстояние от точки до прямой равно длине отрезка, проведенного перпендикулярно из точки к этой прямой. ВМ⊥МЕ и является проекцией наклонной СМ. По т. о 3-х перпендикулярах СМ⊥МЕ и является искомым расстоянием. ВМ=8 см, СВ=6 см ⇒ ∆ ВСМ - египетский. СМ=10 см ( можно проверить по т.Пифагора).

Хороший ответ

28 декабря 2022 23:54

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В кубе ABCDA1B1C1D1 найдите угол между скрещивающимися упрямыми BB1 и AC. Пожалуйся, очень нужно! Большое спасибо заранее)... Какой четырехугольник называется трапецией? Как называются стороны трапеции... найти площадь полной поверхности правильной четырехугольной призмы abcda1b1c1d1 если её диагональ b1d равная 8 см составляет с основанием abcd угол 60... В прямоугольном треугольнике высота, проведенная из вершины прямого угла, равна медиане, проведенной из того же угла. Гипотенуза этого треугольника ра... Умоляю помогите срочно!!!!! Окружность и прямая имеют две общие точки если: а) Расстояние от центра окружности до прямой не превосходит радиуса окруж...