Доказать теорему если диагонали параллелограмма перпендикулярны , то этот параллелограмм - ромб

1 ответ

Посмотреть ответы

Megamozg

2205

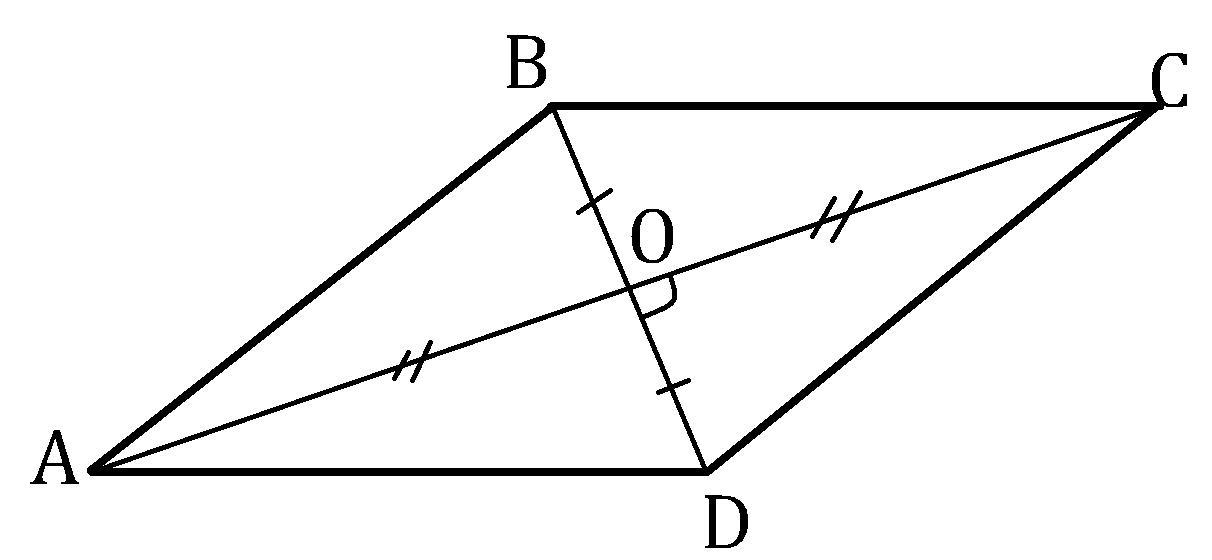
Дано: AB ║ CD; BC ║ DA; AC ⊥ BD.
Доказать: ABCD - ромб.
Решение:AC ∩ BD = O.
AO = OC и BO = OD т.к. диагонали параллелограмма делятся точкой пересечения на два равных отрезка.
Диагонали перпендикулярны, поэтому ΔABO, ΔBCO, ΔCDO и ΔDAO - прямоугольные, эти треугольники равны по двум катетам BO = OD и AO = OC. У равных треугольников соответственные стороны равны, поэтому их гипотенузы равны, а именно AB = BC = CD = DA. Параллелограмм, у которого все стороны равны, является ромбом, что и требовалось доказать.

Хороший ответ

29 декабря 2022 08:05

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

отрезок AD биссектриса треугольника ABC. Через точку D проведена прямая, пересекающая сторону AB в точке E так что AE = ED. Найдите углы треугольника... 1.Стороны параллелограмма равны 12 см и 9 см, а его площадь равна 36 см2. Найдите высоты параллелограмма. 2.В прямоугольном треугольнике с острым угло... В равнобедренном треугольнике АВС медианы пересекаются в точке О.Найдите расстояние от точки О до вершины A если АВ=АС=13см,ВС=10см.... Есть координаты векторов a→ иb→. Определи координаты векторов a→+b→ иb→−a→.... Даю 50 баллов! Составить уравнение плоскости по трем точкам: А(6;0;0), М(-3;3√3;5), В(0;6√3;0). РЕШЕНИЕ необходимо с помощью СИСТЕМЫ УРАВНЕНИЙ (пример...