Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
27 декабря 2022 12:59
939
Найдите углы трапеции. нужно хотя бы 5 заданий! помогите пожалуйста((
1
ответ
1. Сумма углов, прилежащих к боковой стороне трапеции, равна 180°, следовательно
∠В = 180° - 70° = 110°
∠С = 180° - 50° = 130°
2. Трапеция равнобедренная, значит углы при основаниях равны:
∠М = ∠F = 100°
∠E = ∠N = 180° - 100° = 80°
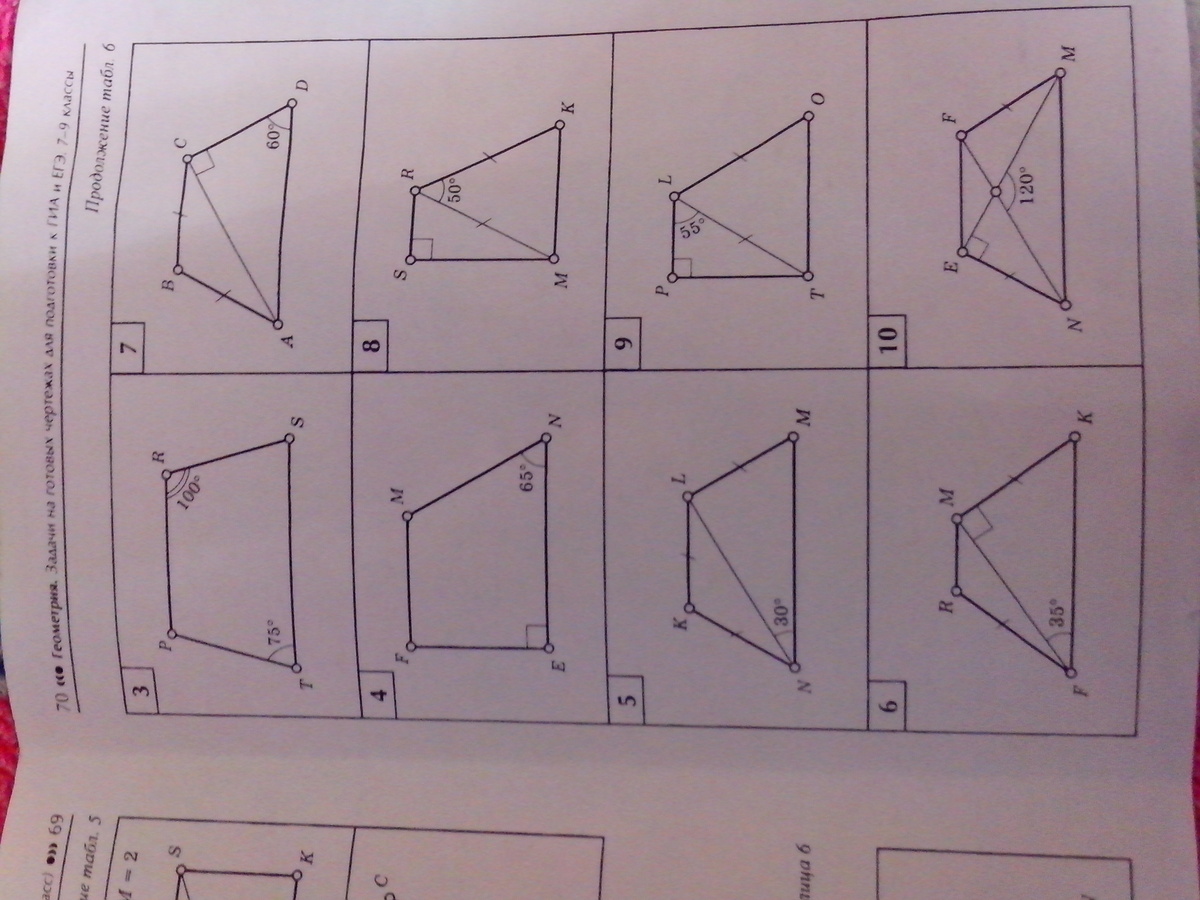
3. Сумма углов, прилежащих к боковой стороне трапеции, равна 180°, следовательно
∠Р = 180° - 75° = 105°
∠S = 180° - 100° = 80°
4. Трапеция прямоугольная, значит
∠F = ∠E = 90°
∠M = 180° - 65° = 115°
5. ∠KLN = ∠MNL = 30° как накрест лежащие при пересечении параллельных KL и MN секущей NL,
ΔNKL равнобедренный, значит углы при основании равны:
∠KNL = ∠KLN = 30°, ⇒ в трапеции
∠N = 60°, ∠M = ∠N = 60°как углы при основании равнобедренной трапеции,
∠K = ∠L = 180° - 60° = 120° (прилежащие к боковой стороне, см. 1)
6. ΔFMK: ∠M = 90°, ∠F = 35°, ⇒∠K = 90° - 35° = 55°
Трапеция равнобедренная, значит в ней:
∠F = ∠K = 55°
∠R = ∠M = 180° - 55° = 125°
7. ΔACD: ∠C = 90°, ∠B = 60°, ⇒ ∠A = 30°
∠BCA = ∠DAC = 30° как накрест лежащие при пересечении параллельных BC и AD секущей AC,
ΔBCA равнобедренный, ⇒
∠ВАС = ∠ВСА = 30°.
Значит ∠BAD = 30° · 2 = 60°. ⇒ трапеция равнобедренная.
В трапеции ∠В = ∠С = 180° - 60° = 120°
8. Трапеция прямоугольная,
∠S = ∠M = 90°.
ΔMRK - равнобедренный, ∠RMK = ∠RKM = (180° - 50°)/2 = 65°
В трапеции ∠К = 65°, тогда
∠R = 180° - 65° = 115° как прилежащие к боковой стороне.
9. Трапеция прямоугольная,
∠Р = ∠Т = 90°.
Из треугольника LPT ∠Т = 90° - 55° = 35°, тогда
∠LTO = ∠LOT = 90° - 35° = 55°
В трапеции ∠L = 180° - 55° = 125°
10. ΔNEM = ΔMFN по гипотенузе и катету (MN - общая, EN = FM), ⇒
∠FNM = ∠EMN и ΔOMN - равнобедренный. (О - точка пересечения диагоналей)
∠OMN = ∠ONM = (180° - 120°)/2 = 30°
ΔENM: ∠E = 90°, ∠M = 30°, ⇒ ∠N = 60°
Трапеция равнобедренная, значит в ней:
∠M = ∠N = 60°
∠E = ∠F = 180° - 60° = 120°
∠В = 180° - 70° = 110°
∠С = 180° - 50° = 130°
2. Трапеция равнобедренная, значит углы при основаниях равны:
∠М = ∠F = 100°
∠E = ∠N = 180° - 100° = 80°
3. Сумма углов, прилежащих к боковой стороне трапеции, равна 180°, следовательно
∠Р = 180° - 75° = 105°
∠S = 180° - 100° = 80°
4. Трапеция прямоугольная, значит
∠F = ∠E = 90°
∠M = 180° - 65° = 115°
5. ∠KLN = ∠MNL = 30° как накрест лежащие при пересечении параллельных KL и MN секущей NL,
ΔNKL равнобедренный, значит углы при основании равны:
∠KNL = ∠KLN = 30°, ⇒ в трапеции
∠N = 60°, ∠M = ∠N = 60°как углы при основании равнобедренной трапеции,
∠K = ∠L = 180° - 60° = 120° (прилежащие к боковой стороне, см. 1)
6. ΔFMK: ∠M = 90°, ∠F = 35°, ⇒∠K = 90° - 35° = 55°
Трапеция равнобедренная, значит в ней:
∠F = ∠K = 55°
∠R = ∠M = 180° - 55° = 125°
7. ΔACD: ∠C = 90°, ∠B = 60°, ⇒ ∠A = 30°
∠BCA = ∠DAC = 30° как накрест лежащие при пересечении параллельных BC и AD секущей AC,
ΔBCA равнобедренный, ⇒
∠ВАС = ∠ВСА = 30°.
Значит ∠BAD = 30° · 2 = 60°. ⇒ трапеция равнобедренная.
В трапеции ∠В = ∠С = 180° - 60° = 120°
8. Трапеция прямоугольная,
∠S = ∠M = 90°.
ΔMRK - равнобедренный, ∠RMK = ∠RKM = (180° - 50°)/2 = 65°
В трапеции ∠К = 65°, тогда
∠R = 180° - 65° = 115° как прилежащие к боковой стороне.
9. Трапеция прямоугольная,
∠Р = ∠Т = 90°.
Из треугольника LPT ∠Т = 90° - 55° = 35°, тогда
∠LTO = ∠LOT = 90° - 35° = 55°
В трапеции ∠L = 180° - 55° = 125°
10. ΔNEM = ΔMFN по гипотенузе и катету (MN - общая, EN = FM), ⇒
∠FNM = ∠EMN и ΔOMN - равнобедренный. (О - точка пересечения диагоналей)
∠OMN = ∠ONM = (180° - 120°)/2 = 30°
ΔENM: ∠E = 90°, ∠M = 30°, ⇒ ∠N = 60°
Трапеция равнобедренная, значит в ней:
∠M = ∠N = 60°
∠E = ∠F = 180° - 60° = 120°
0
·
Хороший ответ
29 декабря 2022 12:59
Остались вопросы?
Еще вопросы по категории Геометрия
Хорды AB и CD пересекаются в точке F так, что BF =16см, AF=4см, CF=DF. найдите CD Пожалуйста срочно...
Луч,дополнительные лучи,плоскость и полуплоскость...
Какие из следующих утверждений верны? 1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны. 2) Если радиусы двух ок...
геометрия 11 класс...............
1. Сумма вертикальных углов AND и CNB , образованных при пересечении прямых AB и CD, равна 208º . Найдите угол ANC 2. Угол, противолежащий основанию р...