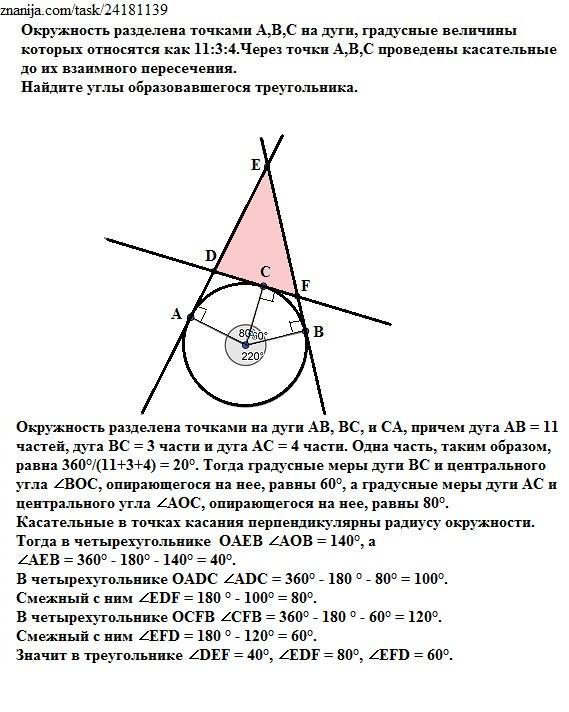
Окружность разделена точками А,Б,С на дуги, градусные величины которых относятся как 11:3:4.Через точки А,Б,С проведены касательные до их взаимного пересечения.Найдите углы образовавшегося треугольника.Помогите пожалуйста!!!Очень надо

Ответ:

Объяснение:
Окружность разделена точками на дуги АВ, ВС, и СА, причем дуга АВ = 11 частей, дуга ВС = 3 части и дуга АС = 4 части. Одна часть, таким образом, равна 360°/(11+3+4) = 20°. Тогда градусные меры дуги ВС и центрального угла ∠ВОС, опирающегося на нее, равны 60°, а градусные меры дуги АС и центрального угла ∠АОС, опирающегося на нее, равны 80°.
Касательные в точках касания перпендикулярны радиусу окружности.
Тогда в четырехугольнике ОАЕВ два угла по 90°, а ∠АОВ = 140°, поэтому ∠АЕВ = 360° - 180° - 140° = 40°.
В четырехугольнике OADC ∠АDС = 360° - 180 ° - 80° = 100°.
Смежный с ним ∠EDF = 180 ° - 100° = 80°.
В четырехугольнике OCFB ∠CFB = 360° - 180 ° - 60° = 120°.
Смежный с ним ∠EFD = 180 ° - 120° = 60°.
Значит в треугольнике ∠DEF = 40°, ∠ЕDF = 80°, ∠EFD = 60°.