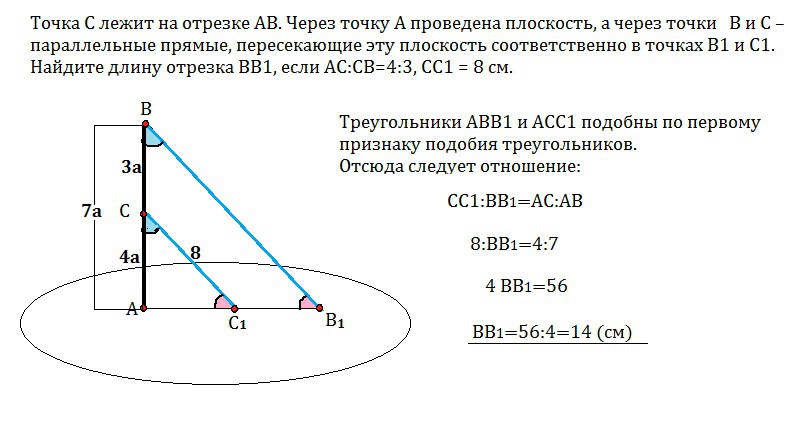
Точка С лежит на отрезке АВ. Через точку А проведена плоскость, ачерез точки В и С – параллельные прямые, пересекающие эту плоскость
соответственно в точках В1 и С1. Найдите длину отрезка ВВ1, если
АС:СВ=4:3, СС1 = 8 см.

1 ответ

Посмотреть ответы

DevAdmin

1720

Точка С лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С – параллельные прямые, пересекающие эту плоскость соответственно в точках В1 и С1.
Найдите длину отрезка ВВ1, если АС:СВ=4:3, СС1 = 8 см.
––––––––––
Через две параллельные прямые можно провести плоскость, притом только одну. ⇒
ВВ1 и СС1 лежат в одной плоскости.
Точки А, В, С. принадлежат отрезку АВ. ⇒ АВ ∈ той же плоскости.
Плоскость, проведенная через А, и плоскость, содержащая СС1 и ВВ1, пересекаются по прямой. АВ1.
Соответственные углы при параллельных прямых и секущей равны. ⇒
∠АСС1= ∠АВВ1, ∠АС1С=∠АВ1В ⇒
∆ АСС1~∆ АВВ1 по первому признаку подобия треугольников.
Пусть коэффициент отношения отрезков АС:ВС будет а.
Тогда АВ=7а
Из подобия следует отношение:
АВ:АС=ВВ1:СС1
7:4=ВВ1:8
4 ВВ1=56⇒
ВВ1=14

Хороший ответ

17 января 2023 03:36

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Площадь боковой поверхности правильной четырехугольной пирамиды SABCD равна 108, а площадь полной поверхности этой пирамиды равна 144. Найдите площадь... В ромбе ABCD биссектриса угла BAC пересекает сторону BC в точке M.Найдите углы ромба, если угол AMC=120* *-градус... Перпендикуляр, проведённый из точки окружности к диаметру, делит его на два отрезка, один из которых относится к диаметру как 9:25. Длина меньшей хорд... Даны две противоположные вершины квадрата А(3;0) и С(-4; 1). Найти две его другие вершины... Треугольник apd и трапеция abcd имеют общую сторону ad и лежат в разных плоскостях. Через основание BC трапеции и середину отрезка pd-точку k проведен...