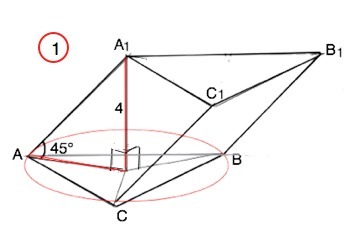
1) В наклонной треугольной призме основанием служит правильный треугольник. Одна из вершин верхнего основания треугольника проектируется в центр нижнего. Боковые ребра призмы составляют с плоскостью основания угол 45 градусов. Найдите объем призмы, если ее высота равна 4.2) В наклонном параллелепипеде площади двух боковых граней равны 20 и 30 см^2, а угол между ними 60 градусов. Найдите объем параллелепипеда, если его боковое ребро равно 5 см.

1) Проекция О вершины верхнего основания - центр нижнего и является центром описанной около нижнего основания окружности.⇒
Отрезок А1О – высота призмы.
АО - катет прямоугольного ∆ АОА1.
АО=А1О:tg45°=4
АО - радиус R описанной окружности
R=a/√3⇒
a=R•√3=4√3
V(призмы)=S (ABC)•A1O
S(ABC)=(4√3)²•√3/4=12√3
V=12√3•4=48√3 (ед. площади)
——————————
Угол между боковыми гранями - двугранный и равен его линейному углу.Из вершины D возведем отрезок DM⊥CC1. Из т.M перпендикулярно к CC1 проведем луч до пересечения с ВВ1 в точке К
Угол DMK- данный и равен 60°.
DM перпендикулярна противоположным сторонам грани ВВ1С1С и является высотой параллелограмма DD1С1С. ⇒
DМ=Ѕ(DD1С1С): ВВ1
DМ=30:5=6 см
Аналогично КM=Ѕ(ВВ1С1С):СС1=20:5=4 см
"Отрежем" от исходной наклонной призмы треугольную призму КМСВ и параллельным переносом установим ее на верхнее основание наклонной призмы. Вследствие этого получим прямую призму АDMKK1M1D1A1. объём которой равен объёму исходной.
V=АА1•S(ADMK)
S(ADMK)=KM•DM•sin60°=4•6•√3/2=12√3
V=5•12√3=60√3