Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
15 января 2023 09:43
1074
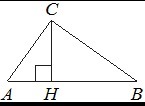
На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=64. Найдите CH
1
ответ
Ответ:16
Объяснение:
Рассмотрим треугольники ACH и BCH. Докажем, что это подобные треугольники: ∠AHC=∠BHC=90° (так как CH - высота). По теореме о сумме углов треугольника: 180°=∠CAH+∠AHC+∠HCA 180°=∠CAH+90°+∠HCA 90°=∠CAH+∠HCA ∠CAH=90°-∠HCA Заметим, что: ∠BCH=90°-∠HCA Получается, что ∠CAH=∠BCH Тогда, по первому признаку подобия, данные треугольники подобны, т.е. можем записать пропорцию: AH/CH=CH/BH AH*BH=CH2 4*64=CH2 256=CH2 CH=√256=16 Ответ: 16
Объяснение:
Рассмотрим треугольники ACH и BCH. Докажем, что это подобные треугольники: ∠AHC=∠BHC=90° (так как CH - высота). По теореме о сумме углов треугольника: 180°=∠CAH+∠AHC+∠HCA 180°=∠CAH+90°+∠HCA 90°=∠CAH+∠HCA ∠CAH=90°-∠HCA Заметим, что: ∠BCH=90°-∠HCA Получается, что ∠CAH=∠BCH Тогда, по первому признаку подобия, данные треугольники подобны, т.е. можем записать пропорцию: AH/CH=CH/BH AH*BH=CH2 4*64=CH2 256=CH2 CH=√256=16 Ответ: 16
0
·
Хороший ответ
17 января 2023 09:43
Остались вопросы?
Еще вопросы по категории Геометрия
Найдите cos a, если sin a = 3/5...
Диагональ прямоугольной трапеции перпендикулярна боковой стороне,острый угол трапеции равен 45 градусов,а её большее основание 14 см.Найдите меньшее о...
Найди площадь сечения прямой призмы плоскостью (AB1C), если AA1=7, AC=10 и AB=26...
Произвольный треугольник имеет два равных угла. Третий угол в этом треугольнике равен 31°. Из равных углов проведены биссектрисы. Найди больший угол,...
Радиус окружности,вписанной в основание правильной четырехугольной пирамиды,равен 3 корня из 2,а длина бокового ребра пирамиды равна 10.Найдите высоту...