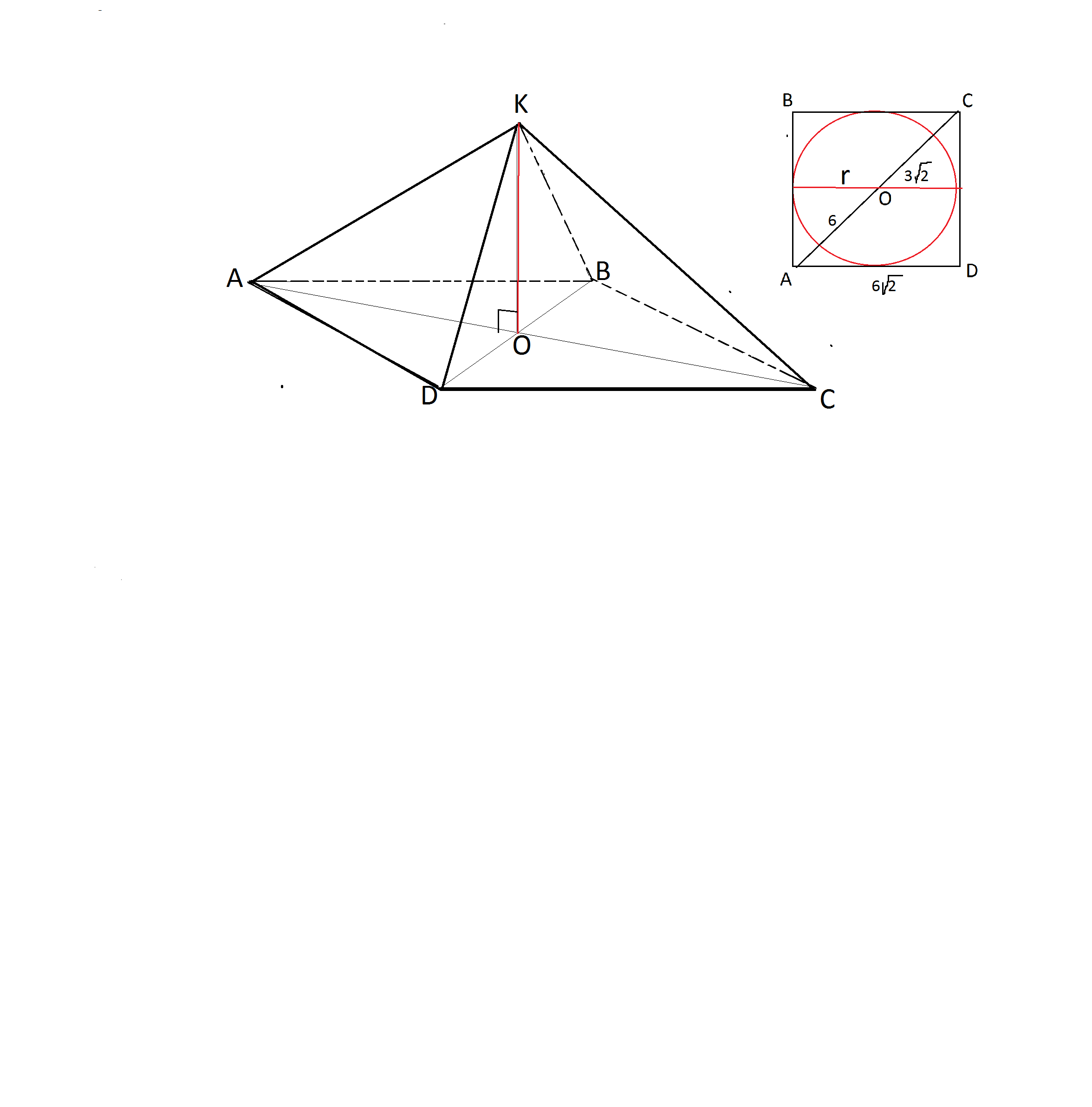
Радиус окружности,вписанной в основание правильной четырехугольной пирамиды,равен 3 корня из 2,а длина бокового ребра пирамиды равна 10.Найдите высоту пирамиды

1 ответ

Посмотреть ответы

DevAdmin

1720

Основанием правильной четырехугольной пирамиды является квадрат.

Радиус вписанной в квадрат окружности равен половине его стороны.

Следовательно, сторона квадрата равна
2r=6√2.

Основание высоты правильной четырехугольной пирамиды находится в центре квадрата - в центре О вписанной окружности.

Высоту КО найдем из прямоугольного треугольника, образованного
ребром АК пирамиды - гипотенуза;
половина АО диагонали квадрата - катет;
высота КО -катет.

Диагональ основания D равна а√2 и
АС равна 6√2·√2=12,
ее половина АО - 6

По теореме Пифагора найдем высоту:
Н=√(АК² -АО²)=√(100-36)=8

Хороший ответ

4 апреля 2023 13:51

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

как сокращать большие дроби? Я знаю как сокращать , но не знаю как сокращать дроби по типу 550/418 или 3255/3720. Может есть какой-то лайфхак?... В правильной шестиугольной призме ABCDEFA1B1C1d1E1F1 все ребра равны 34. Найдите угол D1DF1 . Ответ дайте в градусах.... С какими из предложенных измерений сторон может существовать треугольник? 1) 13 см, 13 см, 30 см 2) 70 см, 20 см, 20 см 3) 80 см, 40 см, 20 см 4) 3... Помогите решить!!!Дан параллелепипед ABCDA1B1C1D1. Докажите, что: а) DC⊥B1C1, и AB⊥A1D1 если ∠BAD =90°; б) АВ⊥СС1 и DD1⊥A1B1, если AB⊥DD1.... Пусть A,B,C углы треугольника. Докажите, что sinA*sinB-cosC=cosA*cosB...