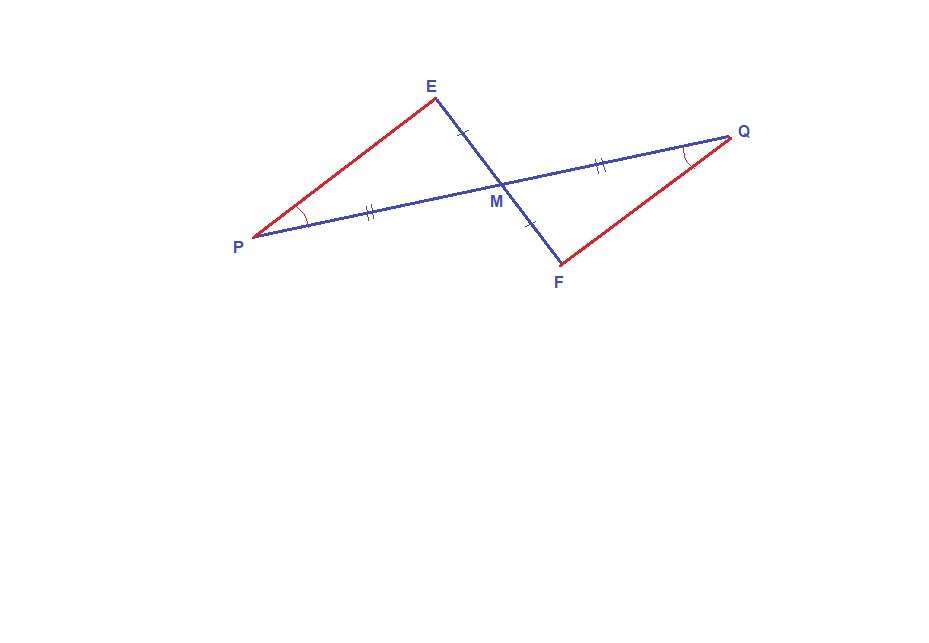
Отрезки EF и PQ пересекаются в их середине M.Докажите что PE паралельна QF.Решите пж с подробным решением.

PM = MQ, EM = MF, так как М - общая середина данных отрезков,
∠РМЕ = ∠QMF как вертикальные, ⇒
ΔРМЕ = ΔQMF по двум сторонам и углу между ними.
В равных треугольниках напротив равных сторон лежат равные углы:
∠ЕРМ = ∠FQM, а эти углы - накрест лежащие при пересечении прямых РЕ и QF секущей PQ, значит
РЕ ║ QF