Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
30 ноября 2022 04:24
2752
Сформулируйте и докажите теорему, выражающую третий признак подобия треугольников.
1
ответ
Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Дано: ΔАВС, ΔА₁В₁С₁,

Доказать: ΔАВС подобен ΔА₁В₁С₁.
Доказательство:
На стороне АС треугольника АВС отложим СА₂ = С₁А₁ и проведем А₂В₂║АВ.
Так как прямая, параллельная стороне треугольника, отсекает треугольник, подобный данному, то
ΔАВС подобен ΔА₂В₂С , значит их стороны пропорциональны:
 , а так как А₂С = А₁С₁, то получаем
, а так как А₂С = А₁С₁, то получаем
 ,
,
По условию:
 .
.
Из этих двух равенств следует, что
А₂В₂ = А₁В₁ и В₂С = В₁С₁.
Тогда ΔА₁В₁С₁ = ΔА₂В₂С по трем сторонам.
Значит,
ΔАВС подобен ΔА₁В₁С₁.
Дано: ΔАВС, ΔА₁В₁С₁,
Доказать: ΔАВС подобен ΔА₁В₁С₁.
Доказательство:
На стороне АС треугольника АВС отложим СА₂ = С₁А₁ и проведем А₂В₂║АВ.
Так как прямая, параллельная стороне треугольника, отсекает треугольник, подобный данному, то
ΔАВС подобен ΔА₂В₂С , значит их стороны пропорциональны:
По условию:
Из этих двух равенств следует, что
А₂В₂ = А₁В₁ и В₂С = В₁С₁.
Тогда ΔА₁В₁С₁ = ΔА₂В₂С по трем сторонам.
Значит,
ΔАВС подобен ΔА₁В₁С₁.
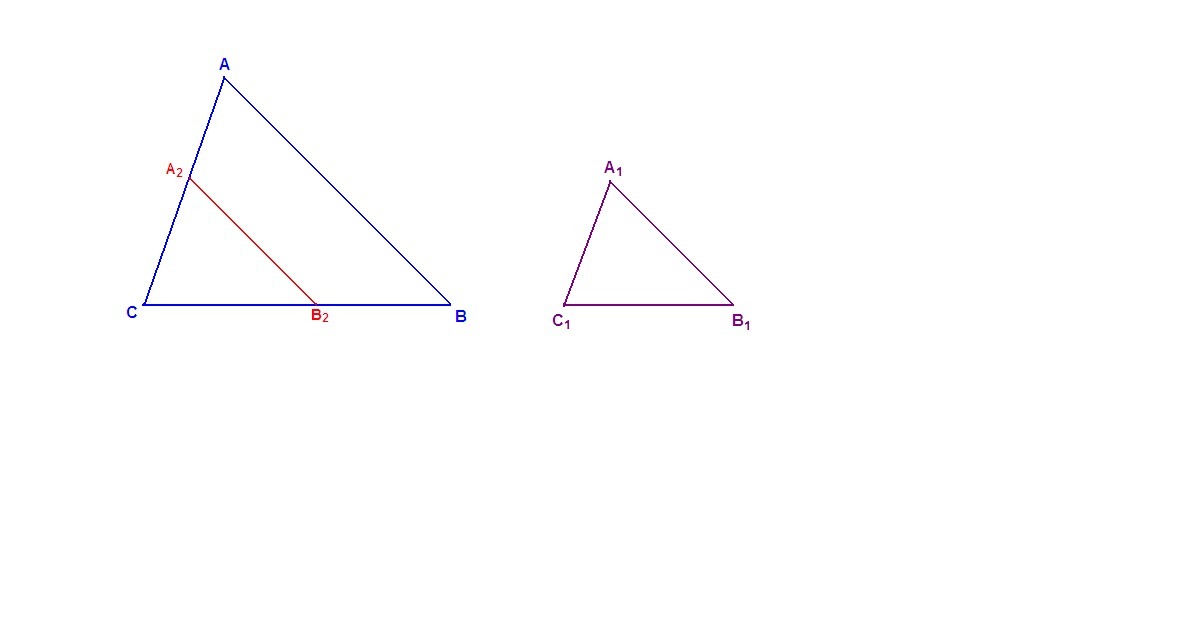
0
·
Хороший ответ
2 декабря 2022 04:24
Остались вопросы?
Еще вопросы по категории Геометрия
Помогите пожалуйста...
На сторонах AВ и AD параллелограмма ABCD отмечены соответственно точки F и К так, что AK = KD, a AF : FB = 1 : 2. Найдите площадь треугольника CFK, ес...
ABCDA1B1C1D1 – параллелепипед. Изобразите на рисунке векторы, равные: 1) DA+CD+B1B+AB ; 2) DB-AB1 . СПАСИБО...
По данным рисунка градусная мера угла 1 - один из корней уравнения (х-152)(х-78)=0, градусная мера угла 2 - один из корней уравнения |5x-832|=|4x-86|...
Вневписанная в треугольник АВС окружность касается его боковой стороны и продолжения основания АС. Докажите, что радиус этой окружности равен высоте В...