Доказательство теоремы о свойстве односторонних углов при пересечении двух параллельных прямых третьей прямой.

Сумма односторонних углов, образованных пересечением двух параллельных прямых третьей, равна 180°.

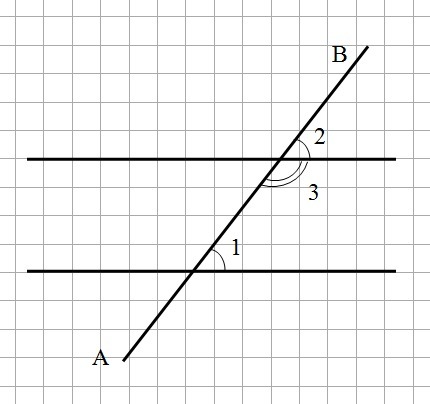
Доказательство: (см. рис.)
Пусть параллельные прямые а и b пересечены секущей АВ.
Тогда соответственные ∠1 и ∠2 будут равны,
∠2 и ∠3 – смежные, поэтому ∠2 + ∠3 = 180°.
Из равенств ∠1 = ∠2 и ∠2 + ∠3 = 180° следует, что
сумма односторонних углов ∠1 + ∠3 = 180°.
Теорема доказана.