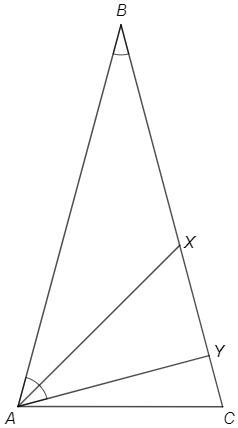
Треугольник ABC стороны AB и BC равны угол ACB равен 75 градусам на стороне BC взяли точки X и Y так что точка X лежит между точками B и Y AX=BX и угол BAX= угол YAX найдите длину отрезка AY если AX=22

1 ответ

Посмотреть ответы

Megamozg

2205

AB=BC, △ABC - р/б => ∠BAC=∠ACB =75°
∠B =180°-75°·2 =30°
AX=BX=22, △AXB - р/б => ∠B=∠BAX =30°
∠BAX=∠YAX =30°
∠BAY=∠BAX+∠YAX =60°
△BAY: ∠AYB=180°-∠BAY-∠B =180°-60°-30° =90°
△XAY: XY=AX/2 =22/2 =11 (катет против угла 30°)
AY=√(AX^2 -XY^2) =√(22^2 -11^2) =√(11*33) =11√3 (т Пифагора)

Хороший ответ

17 января 2023 10:29

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найти катеты прямоугольного треугольника,если гипотенуза равна 4 см,а косинус одного из углов 0,6.... Какая формула для вычисления радиуса окружности, вписанной в выпуклый многоугольник, подскажите, пожалуйста... Обчислить: 1) 4 cos 90° + 2 cos 180° - tg 180°; 2) cos 0° - cos 180° + sin 90°.... проведите прямую, обозначьте ее буквой m. Отметьте точки А и В, лежащие на этой прямой ,и точки С, D,E,не лежащие на ней .... Треугольники ABC и ABD не лежат в одной плоскости. Докажите, что любая прямая, параллельная отрезку CD, пересекает плоскости данных треугольников. (ри...