. Найдите площадь квадрата, если его диагональ равна 1.

2 ответа

Посмотреть ответы

v.petrogradov

Ответ:
1/2 (кв. единиц)
Объяснение:
Пусть сторона квадрата x единиц. Тогда площадь S квадрата, как известно, равна:
S = x².
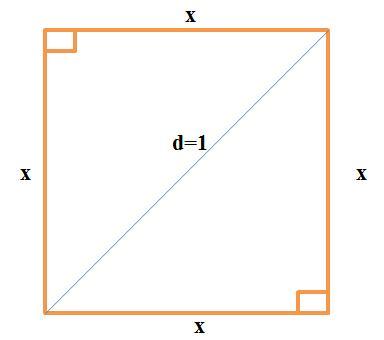
Диагональ d=1 (единиц) квадрата делит квадрат на 2 прямоугольные треугольники (см. рисунок), для которых диагональ d - это гипотенуза. По теореме Пифагора получим:
d²=x²+x².
Отсюда 2·x²=d² или x²=d²/2=1/2. В силу этого получим:
S = 1/2 (кв. единиц).

Хороший ответ

1 сентября 2022 20:58

m.pozharskiy

Условие: Найдите площадь квадрата, если его диагональ равна 1.
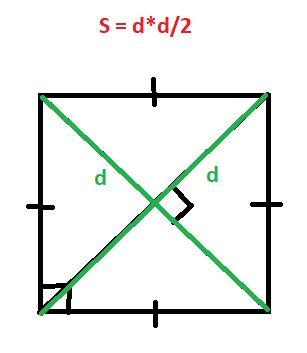
Квадрат есть частный случай ромба, у которого все углы прямые.
Площадь ромба равна половине произведения его диагоналей.
Но у квадрата длины диагоналей равны, поэтому площадь квадрата будет равна:
$S=\dfrac=\dfrac=\dfrac$
Подставляем d = 1 и получаем ответ:
$\boldsymbol=\dfrac=\dfrac}$

1 сентября 2022 20:58

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Напишите все свойства и признаки равнобедренного треугольника, ВСЕ!... В треугольнике ОАВ стороны ОА и АВ равны, точка С- середина стороны ОА, АВ =20см. Разность периметров треугольников АСВ и ОСВ равна 8см. найдите сторо... Касательная к вписанной окружности треугольника ABC пересекает стороны AC и BC в точках D и K соответственно. Известно, что AB=8 см, BC=10 см, AC=14 с... Геометрия. 8 класс помогите #uztest... Помогите решить подробно задачу...

. Най­ди­те пло­щадь квад­ра­та, если его диа­го­наль равна 1.

. Найдите площадь квадрата, если его диагональ равна 1.